Feledatok analízisből

1. Számítsuk ki a következő határértéket!

$$\lim_{n \rightarrow \infty} \left( \frac{3+2n}{2n-5}\right) ^{4n+7}$$

Ennek a feladatnak az alapja a következő határérték:

$$\lim_{n \rightarrow \infty} \left( 1+ \frac{1}{n}\right) ^n = e$$

Itt az e az Euler-szám, amit a számológépen is meg lehet találni a logaritmus billentyűk környékén, és shift vagy 2ndF gombokkal lehet előhozni. Ha a határértékben egy kicsi módosítást teszünk, azaz az 1-est kicseréljük x-re, akkor a végeredményben az e-nek is x lesz a kitevője:

$$\lim_{n \rightarrow \infty} \left( 1+ \frac{\color{red}{x}}{n}\right) ^n = e^\color{red}{x}$$

Most térjünk vissza az eredeti feladathoz. A cél az, hogy ilyen alakúra hozzuk. Láthatjuk, hogy a zárójelen belül kétszer is szerepel a 2n:

$$\lim_{n \rightarrow \infty} \left( \frac{3+\color{red}{2n}}{\color{red}{2n}-5}\right) ^{4n+7}$$

Ezért emeljük ki a tört felső és alsó részéről is a 2n-t

$$\require{cancel} \lim_{n \rightarrow \infty} \left( \frac{\cancel{\color{red}{2n}}(\frac{3}{2n}+1)}{\cancel{\color{red}{2n}}(1-\frac{5}{2n})}\right) ^{4n+7}$$

Mivel a tört felső és alsó részében is szerepel ugyanaz a dolog szorzatban (a 2n), ezért ez kiesik. Még egy dolgot megváltoztattam: a felső részben megfordítottam az összeadás sorrendjét:

$$\lim_{n \rightarrow \infty} \left( \frac{1+\frac{3}{2n}}{1-\frac{5}{2n}}\right) ^{4n+7}$$

A következő, amit észrevehetünk, az a kitevőben lévő összeadás. Erre van egy ilyen szabály:

$$\color{ForestGreen}{a}^{\color{DarkOrange}{n}+\color{DarkMagenta}{m}}=\color{ForestGreen}{a}^\color{DarkOrange}{n} \cdot \color{ForestGreen}{a}^\color{DarkMagenta}{m}$$

Ezt a szabályt a feladatban lévő 4n+7 kitevőre alkalmazzuk. (Az a-nak a zárójeles rész felel meg.)

$$\lim_{n \rightarrow \infty} \color{ForestGreen}{\left( \frac{1+\frac{3}{2n}}{1-\frac{5}{2n}}\right)} ^{\color{DarkOrange}{4n}} \cdot \color{ForestGreen}{\left( \frac{1+\frac{3}{2n}}{1-\frac{5}{2n}}\right)} ^{\color{DarkMagenta}{7}}$$

Nézzük meg külön a szorzat második részét:

$$\lim_{n \rightarrow \infty} \left( \frac{1+\frac{3}{2n}}{1-\frac{5}{2n}}\right) ^{7}$$

Ennek a kitevője 7, ezért nem tart végtelenhez. A zárójelen belüli részt kell megnézni, hogy mi a határértéke. Az $\frac 1n$ sorozat határértéke 0, ezért:

$$\require{cancel} \lim_{n \rightarrow \infty} \left( \frac{1+\cancelto{0}{\frac{3}{2n}}}{1-\cancelto{0}{\frac{5}{2n}}}\right) ^{7} = \left(\frac{1}{1}\right)^7 = 1$$

Visszatérhetünk a szorzat másik részéhez. Ennek a kitevője 4n, ami 2 ⋅ 2n. Miért jó, hogy így írom? Mert megint van egy hatványozós szabály, mégpedig:

$$\color{ForestGreen}{a}^{\color{DarkOrange}{n}\cdot \color{DarkMagenta}{m}}=(\color{ForestGreen}{a}^\color{DarkOrange}{n})^\color{DarkMagenta}{m}$$

Tehát a kitevőben lévő szorzatból dupla hatványozás lesz. Így ezt kapjuk:

$$\lim_{n \rightarrow \infty} \color{ForestGreen}{\left( \frac{1+\frac{3}{2n}}{1-\frac{5}{2n}}\right)} ^{\color{DarkMagenta}{2}\cdot \color{DarkOrange}{2n}} = \lim_{n \rightarrow \infty} \left(\color{ForestGreen}{\left( \frac{1+\frac{3}{2n}}{1-\frac{5}{2n}}\right)} ^{\color{DarkOrange}{2n}} \right)^{\color{DarkMagenta}{2}}$$

Még egy lépés van hátra: a belső zárójelben a törtet kettészedhetjük: külön a számlálót, külön a nevezőt hatványozzuk:

$$\lim_{n \rightarrow \infty} \left(\frac{(1+\frac{3}{2n})^{2n}}{(1-\frac{5}{2n})^{2n}} \right)^2$$

A nagy tört számlálójában (felső rész) a pirossal írt rész egyaránt 2n. Ugyanez az alsó részben kékkel van írva.

$$\lim_{n \rightarrow \infty} \left(\frac{(1+\frac{3}{\color{red}{2n}})^{\color{red}{2n}}}{(1-\frac{5}{\color{blue}{2n}})^{\color{blue}{2n}}} \right)^2$$

Emiatt a határértékre használhatjuk a bevezetőben felírt e ^x-es határértéket. Az x értéke felül 3, alul pedig -5:

$$\lim_{n \rightarrow \infty} \left(\frac{(1+\frac{3}{2n})^{2n}}{(1-\frac{5}{2n})^{2n}} \right)^2 = \left( \frac{e^3}{e^{-5}}\right)^2=(e^8)^2=e^{16}$$

Az utolsó lépésekben már csak a hatványozás szabályit kellett használni.

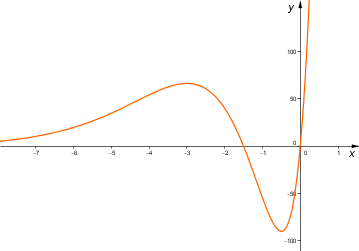
2. Végezzünk teljes függvényvizsgálatot!

$$f(x) = (2x^2+3x)e^{x+5}$$

Mivel kezdjük a feladatot? Legelőször azzal, hogy megnézzük, hol van értelmezve, azaz x helyére milyen számot írhatunk. Nincs olyan szám, amire ne lenne értelmezve, ezért $x \in \mathbb{R}$.

Nézhetjük a tengelymetszeteket: ahol az x-tengelyt metszi, az a zérushely. Ezt úgy kapjuk meg, ha f(x) = 0:

$(2x^2+3x)e^{x+5} = 0$

Egy szorzat akkor 0, ha valamelyik tagja nulla, mert valamiszer 0 az 0. Az e-s rész nem lehet 0, mert az exponenciális függvény mindig pozitív. Akkor csak a zárójeles rész lehet 0:

$2x^2+3x = 0$

Ezt a másodfokú egyenletet megoldhatjuk megoldóképlettel is, de jobb, ha kiemelünk x-et:

$x(2x+3) = 0$

Így megint szorzatot kaptunk, ami akkor 0, ha valamelyik tag 0. Tehát vagy

$x = 0,$

vagy

$2x+3 = 0 \qquad \textrm{azaz} \quad x=-\frac 32$

Most az y-tengelymetszet jön: ehhez x helyére 0-t kell írni:

$(2 \cdot 0^2+ 3 \cdot 0)e^{0+5}= 0 \cdot e^5 = 0$

Tehát az y-tengelyt az y = 0 pontban metszi.

Megnézhetjük a függvény határértékeit a végtelenben.

$$\lim_{x \rightarrow \infty} (2x^2+3x)e^{x+5} = \infty$$
Végtelenben a zárójeles rész és az e-s rész is végtelenhez tart, nyilván a szorzatuk is (mert végtelenszer végtelen az végtelen).
$$\lim_{x \rightarrow -\infty} (2x^2+3x)e^{x+5}$$
Mínusz végtelenben már baj van, mert a zárójel most is végtelenbe tart, de az exponenciális rész 0-hoz, és végtelenszer 0 nem eldönthető. Ezért L'Hospital (lopitál) szabályt kell alkalmazni. De az csak törteknél működik, amikor $\frac 00$ vagy $\frac {\infty}{\infty}$ jön ki. Csináljunk törtet a függvényből!
$$\lim_{x \rightarrow -\infty} \frac{2x^2+3x}{e^{-(x+5)}}$$
Az e-s részt levittem a nevezőbe, és kapott egy mínuszt. L'Hospital szabálynál ugye deriválni kell a felső részt és az alsó részt külön:
$$\lim_{x \rightarrow -\infty} \frac{2x^2+3x}{e^{-(x+5)}} = \lim_{x \rightarrow -\infty} \frac{4x+3}{-e^{-(x+5)}}$$
Most a felső rész -∞-hez tart, az alsó szintén, mert a kitevőben -(-∞) = ∞ van, és még az e előtt is van mínusz. Így megint $\frac {\infty}{\infty}$ lett. Akkor lopitáljunk még egyszer:
$$\lim_{x \rightarrow -\infty} \frac{4x+3}{-e^{-(x+5)}} = \lim_{x \rightarrow -\infty} \frac{4}{e^{-(x+5)}}= \frac{4}{\infty} = 0$$
Ez már jó, mert a számláló 4, a nevező pedig végtelenhez tart, és szám per végtelen az 0.

Tehát a függvény határértéke ∞-ben ∞, -∞-ben 0.

Következő lehet a paritásvizsgálat, azaz hogy páros vagy páratlan-e, vagy egyik se. Ezt úgy tudjuk megnézni, hogy x helyére -x-et írunk. Ha így visszakapjuk az eredeti függvényt, akkor páros, ha a függvény -1-szeresét, akkor páratlan, ha egyiket se, akkor nincs paritása.

$f(-x)=f(x)$	páros
$f(-x)=-f(x)$	páratlan
$f(-x)$ egyik se	nincs paritás

Nézzük, mi a helyzet a függvénnyel:

$f(-x) = (2\cdot (-x)^2+3\cdot(-x))e^{-x+5}=(2x^2-3x)e^{-x+5}$

Ez se az eredetivel nem egyezik meg, se a -1-szeresével, ezért a függvénynek nincs paritása.

Most jöhet a monotonitás és szélsőérték-vizsgálat. Ehhez a függvényt deriválni kell:

$f'(x) = (4x+3)e^{x+5} + (2x^23x)e^{x+5}=(2x^2+7x+3)e^{x+5}$

Ezt kell egyenlővé tenni 0-val:

$(2x^2+7x+3)e^{x+5}=0$

Ez szorzat, ami akkor 0, ha valamelyik tag 0. Már tudjuk, hogy $e^{x+5}$ mindig pozitív, tehát nem lehet 0, marad a zárójeles rész, ami egy másodfokú cucc, ezt meg könnyű megoldani. A megoldás:

$x=-3$

$x=-\frac 12$

Most csinálunk egy táblázatot, amibe az x-re kijött számokat írjuk:

x	x < -3	x = -3	-3 < x < -$\frac 12$	x = -$\frac 12$	-$\frac 12$ < x
f'
f

Úgy kell kitölteni, hogy a második sorba a -3 és a -$\frac 12$ alá 0-t írunk, mert ott f' 0, a többi mezőbe pedig pluszt vagy mínuszt. Pl x < -3 alá pluszt írunk, mert ott f' pozitív. Ezt onnan lehet tudni, hogy x helyére -4-et (vagy bármilyen -3-nál kisebb számot) írunk, és kiszámoljuk.

x	x < -3	x = -3	-3 < x < -$\frac 12$	x = -$\frac 12$	-$\frac 12$ < x
f'	+	0	-	0	+
f

Végül a harmadik sort úgy töltjük ki, hogy minden + alá ↗ nyilat és minden - alá ↘ nyilat írunk:

x	x < -3	x = -3	-3 < x < -$\frac 12$	x = -$\frac 12$	-$\frac 12$ < x
f'	+	0	-	0	+
f	↗		↘		↗

Ahol a felnyíl átmegy lenyílba, ott maximuma van (domb), és ahol a lenyíl átmegy felnyílba, ott minimuma van (gödör). Így a kész táblázat:

x	x < -3	x = -3	-3 < x < -$\frac 12$	x = -$\frac 12$	-$\frac 12$ < x
f'	+	0	-	0	+
f	↗	MAX	↘	MIN	↗

Mellesleg a nyilak jelentés: ↗: a függvény szigorúan monoton növekvő, ↘: szigorúan monoton csökkenő.

Következő lépés a görbület (konvexitás) és az inflexiós pont meghatározása. Ehhez másodszorra is le kell deriválni a függvényt:

$f''(x) = (4x+7)e^{x+5}+(2x^2+7x+3)e^{x+5}=(2x^2+11x+10)e^{x+5}$

Ezt most is 0-ra kell megoldan, és elég csak a zárójeles résszel foglalkozni, ami megint másodfokú. Amegoldások:

$x=-4,35$

$x=-1,15$

Ugyanúgy táblázatot csinálunk és kitöltjük pluszmínuszokkal, de most a plusszok alá ∪-t, a mínuszok alá ∩-t írunk:

x	x < -4,35	x = -4,35	-4,35 < x < -1,15	x = -1,15	-1,15 < x
f''	+	0	-	0	+
f	∪	INFL	∩	INFL	∪

A ∪ jelentése: konvex, itt a függvény mosolyog. A ∩ konkáv, a függvény szomorú. Egy konvex és egy konkáv rész között inflexiós pont van.

Most egy olyan rész jön, amit senki sem szeret: az aszimptotikus viselkedés, ami azt jelenti, hogy hozzásimul-e egy egyeneshez. Ennek a függvénynek csak a végtelenekben kell megnézni, mert mindenhol értelmezve van. Mivel az aszimptota egy egyenes, ezért van meredeksége. Ezt a következő módon számítjuk:

$$m=\lim_{x \rightarrow \pm \infty} \frac{f(x)}{x}$$
f(x) helyére írjuk be a függvényünket:
$$m=\lim_{x \rightarrow \pm \infty} \frac{(2x^2+3x)e^{x+5}}{x}=\lim_{x \rightarrow \pm \infty} (2x+3)e^{x+5}$$
Ez eléggé hasonlít ahhoz, amit az eredeti függvény határértékénél néztünk. Ott az derült ki, hogy a határérték ∞-ben ∞, -∞-ben 0. Ez most is igaz, amiből az következik, hogy a meredekség ∞-ben ∞, tehát nincs olyan egyenes, amihez hozzásimul a függvény. -∞-ben pedig m=0, azaz olyan egyenes, ami az x-tengellyel párhuzamos. Ki kéne még számítani, hogy az egyenes hol metszi az y-tengelyt. Erre is van képlet:
$$b=\lim_{x \rightarrow \pm \infty} (f(x)-mx)$$
Mivel aszimptota csak -∞-ben van, és ott m=0, ezért f(x) határértékét kell kiszámolni (mert f(x) - 0 ⋅ x = f(x)), amit már megtettünk, és 0 jött ki. Tehát az aszimptota az y-tengelyt 0-ban metszi és párhuzamos az x-tengellyel, vagyis maga az x-tengely.

Most már mindent tudunk a függvényről, hogy ábrázolhassuk:

3. Adja meg az

$$\color{DarkMagenta}{y'}+\textrm{ctg } x \cdot \color{DarkGreen}{y} = \sin^3 x$$ differenciálegyenlet általános megoldását!

Nagyon sokféle differenciálegyenlet van, és mindegyiknek más a megoldási módja. Hogyan jöjjünk rá, hogy ezt hogy kell megoldani? Ennek az egyenletnek az alakja ilyen: valami y' + valami y = valami. Egy ilyen egyenletet így oldunk meg:

1. Először az egyenlet jobb oldalát átírjuk 0-ra: $$\color{DarkMagenta}{y'}+\textrm{ctg } x \cdot \color{DarkGreen}{y} = 0$$ Az y'-t átírjuk $\frac{\textrm{d}y}{\textrm{d}x}$-re: $$\frac{\textrm{d}y}{\textrm{d}x}+\textrm{ctg } x \cdot y = 0$$ Az a cél, hogy x-ek csak az egyik oldalon, y-ok csak a másik oldalon legyenek. Ezért a ctg x ⋅ y-t kivonjuk: $$\frac{\textrm{d}y}{\textrm{d}x} = -\textrm{ctg } x \cdot y$$ Átszorzunk dx-szel és osztunk y-nal: $$\frac{1}{y} \textrm{d}y = -\textrm{ctg } x \textrm{ d}x$$ Így már hasonlít valamire, csak hiányzik az elejéről egy integráljel: $$\int \frac{1}{y} \textrm{d}y = \int -\textrm{ctg } x \textrm{ d}x$$ A bal oldalt y szerint, a jobb oldalt x szerint kiintegráljuk: $$\ln |y| = -\ln|\sin x| + C$$ A jobb oldalra került egy konstans, az integrálás miatt. Mindkét oldalra felesleges kiírni, mert akkor ki lehetne vonni az egyiket a másikból, ami ugyanúgy egy konstans. Másrészt y-t akarom kifejezni, ehhez az ln-t el kell tüntetni. Ezért a C zavaró, jobb lenne, ha az is ln-es lenn, mert akkor összevonhatnánk a sin x-szel. Ezért C helyett nyugodtan írhatunk ln C-t: $$\ln |y| = -\ln|\sin x| + \ln C =\ln C - \ln|\sin x|$$ $$\ln |y| = \ln\left|\frac{C}{ \sin x}\right|$$ Most már elhagyhatjuk az ln-t, és akár az abszolútértéket is: $$\color{DarkGreen}{y} = \color{DarkGreen}{\frac{C}{ \sin x}}$$ Megkaptuk a 0-ra átírt egyenlet megoldását. De az eredeti differenciálegyenlet jobb oldalán sin³ x volt. Most ezt kéne megoldani. Ehhez jön a 2. lépés:

2. Írjuk át az eredményül kapott C konstanst C(x) függvényre, és deriváljuk y-t: $$\color{DarkGreen}{y} = \color{DarkGreen}{ \frac{C(x)}{ \sin x}}$$ $$\color{DarkMagenta}{y'} =\color{DarkMagenta}{ \frac{C'(x)\cdot \sin x - C(x)\cdot \cos x}{\sin^2 x}}$$ A C(x) ismeretlen függvény, ezért a deriválást csak jelölöm egy vesszővel. Most visszahelyettesítjük y-t és y'-t az eredeti egyenletbe: $$\color{DarkMagenta}{\frac{C'(x)\cdot \sin x - C(x)\cdot \cos x}{\sin^2 x}} + \textrm{ctg } x \cdot \color{DarkGreen}{\frac{C(x)}{ \sin x} }= \sin^3 x$$
Írjuk át a ctg x-et $\color{FireBrick}{\frac{\cos x}{\sin x}}$-re:

$$\color{DarkMagenta}{\frac{C'(x)\cdot \sin x - C(x)\cdot \cos x}{\sin^2 x}} + \color{FireBrick}{\frac{\cos x}{\sin x} }\cdot \color{DarkGreen}{\frac{C(x)}{ \sin x} } = \sin^3 x$$ Az első törtet szedjük ketté, a másik kettőt meg szorozzuk össze: $$\frac{C'(x)\cdot \sin x}{\sin^2 x} - \frac{ C(x)\cdot \cos x}{\sin^2 x} + \frac{\cos x \cdot C(x)}{ \sin^2 x} = \sin^3 x$$ Az első törtben sin x-szel lehet egyszerűsíteni. A második és a harmadik tört ugyanaz, ezért szépen ki is esnek, mert a második előtt mínusz van. Egyébként az ilyen differenciálegyenletek megoldásánál a C(x) mindig kiesik. Ha nem, akkor valamit rosszul csináltunk. Ami marad: $$\frac{C'(x)}{\sin x} = \sin^3 x \quad / \cdot \sin x$$ $$C'(x) = \sin^4 x$$ Azt kaptuk, hogy a C(x) függvény deriváltja sin⁴ x. C(x)-et megkapjuk, ha integrálunk: $$C(x) = \int \sin^4 x \textrm{ d}x$$ Na igen, de hogy integráljuk ki sin⁴ x-et??? Először írjuk át így: (sin²x)². Valahonnan tudhatjuk, hogy sin²x = $\frac{1}{2}$ ⋅ (1 - cos 2x). Ezt kell tehát négyzetre emelni: $$(\sin^2 x)^2 = \left(\frac{1}{2}(1-\cos 2x)\right)^2 = \frac{1}{4}(1 - 2\cdot \cos 2x + \cos^2 2x)$$ Ebben még van egy cos²-es rész, amit megintcsak át lehet írni, hasonlóan a sin²-hez, de itt x helyett 2x van: cos²2x = $\frac{1}{2}$ ⋅ (1 + cos 4x): $$\frac{1}{4}\left(1 - 2\cdot \cos 2x + \frac{1}{2} (1+ \cos 4x)\right)$$ Zárójelfelbontás után: $$\frac 14 - \frac 12 \cdot \cos 2x + \frac 18 + \frac 18 \cdot \cos 4x = \frac 38 - \frac 12 \cdot \cos 2x + \frac 18 \cdot \cos 4x$$ Ezt már könnyebben ki tudjuk integrálni: $$\int \frac 38 - \frac 12 \cdot \cos 2x + \frac 18 \cdot \cos 4x = \frac 38 x - \frac 12 \cdot \frac{\sin 2x}{2} + \frac 18 \cdot \frac{\sin 4x}{4}=$$ $$= \frac 38 x - \frac 14 \cdot\sin 2x + \frac {1}{32} \cdot\sin 4x$$ Így most megkaptuk C(x)-et, de ne feledkezzünk meg az integrációs konstansról, amit most ne C-vel jelöljünk, hanem mondjuk K-val: $$C(x) = \frac 38 x - \frac 14 \cdot\sin 2x + \frac {1}{32} \cdot\sin 4x +K$$ Most már csak egy dolgunk van, visszahelyettesíteni y képletébe C(x) helyére ezt: $$y = \frac 38 \cdot \frac{x}{\sin x} - \frac 14 \cdot\frac{\sin 2x}{\sin x} + \frac {1}{32} \cdot \frac{\sin 4x}{\sin x} + \frac{K}{\sin x}$$ Ez az általános megoldása a differenciálegyenletnek.