Feledatok valószínűségszámításból

1. Egy kisboltba három féle csoki érkezik: mogyorós, mandulás és epres. A csokik 30%-a mogyorós, 25%-a mandulás, a többi epres. Szállítás közben a csokik némelyike eltörik, ezeket akciósan adják el. A mogyorós csokik 9%-a, a mandulások 8%-a, az epresek 3%-a törik el átlagosan. Véletlenszerűen kiválasztok egy leértékelt csoki. Mekkora a valószínűsége, hogy epreset választottam?

A feladat sokkal egyszerűbb, mint elsőre tűnik. Ez egy tipikus feladat, a megoldásához alig kell bármit tudni a valószínűségszámításról. Először csináljunk egy táblázatot az adatokból:

	mogyorós	mandulás	epres
hány %	30%	25%	45%
törött	9%	8%	3%

A valószínűségszámításban események valószínűségét számoljuk ki, ezeket az eseményeket nagy betűvel szokás jelölni. Legyen A₁ az az esemény, hogy mogyorós csokit választunk, A₂, hogy mandulásat, A₃, hogy epreset. T pedig jelentse azt az eseményt, hogy a kiválasztott csoki törött.

Annak a valószínűsége, hogy egy kiválasztott csoki törött, P(T), annak, hogy epres, P(A₃) stb. Hogy kell felírni annak a valószínűségét, amit a feladat kérdez? Mivel már eleve tudjuk, hogy törött csokit választunk, ezt bele kell venni a valószínűségbe, mégpedig így: P(A₃|T). Ezt úgy hívják, hogy feltételes valószínűség.

Nézzük meg, hogy a táblázatban szereplő számok milyen valószínűséget jelentenek. A 30% pl annak a valószínűsége, hogy mogyorós csokit választok. Ez betűkkel így néz ki: P(A₁). A második sorban lévő számok már trükkösebbek. A 9% azt jelenti, hogy mennyi a valószínűsége, hogy törött csokit választok, feltéve, hogy a csoki mogyorós. Hiszen a második sorban minden % a töröttségre vonatkozik, de attól függ, milyen fajta a csoki. Ez betűvel ilyen: P(T|A₁). Töltsük ki ilyen P-kkel a táblázatot:

	mogyorós	mandulás	epres
hány %	P(A1)	P(A2)	P(A3)
törött	P(T|A1)	P(T|A2)	P(T|A3)

A gond az, hogy a táblázatban nem szerepel a kérdezett P(A₃|T) valószínűség. :-( De pont erre találták ki a Bayes-tételt! :-)
$$ P(A_3 | T)= \frac{P(T | A_3)P(A_3)}{P(T)} $$
Még mindig nem lettünk elég okosak, mert most meg a nevezőben van a P(T), ami szintén nincs benne a táblázatban. De ennek a kiszámolására is van képlet, mégpedig a teljes valószínűség tétele: $$ P(T)=\sum_{i=1}^{3}P(T | A_i)P(A_i) $$
De ez mit is akar jelenteni? Írjuk fel szumma jel nélkül: $$ P(T)=\color{#FF8C00}{P(T | A_1)P(A_1)}+\color{#32CD32}{P(T | A_2)P(A_2)} +\color{#9932CC}{P(T | A_3)P(A_3)} $$
ÉS ezek már végre szerepelnek a táblázatban! :-) Most már a betűk helyett írhatjuk a számokat is, de ne %-kal, hanem írjuk át pl. a 30%=0,3. $$ P(T)=\color{#FF8C00}{0,09 \cdot 0,3}+\color{#32CD32}{0,08 \cdot 0,25} +\color{#9932CC}{0,03 \cdot 0,45}= 0,0605 $$
Végül a P(A₃|T) kiszámolásához menjünk vissza a Bayes-tételhez. A nevezőt most számoltuk ki, a számláló pedig a lila betűs rész.
$$ P(A_3 | T)= \frac{\color{#9932CC}{0,03 \cdot 0,45}}{0,0605}=\frac{0,0135}{0,0605}=0,2231=22,31\% $$
Ezzel kész is a feladat.

2. Megválasztható-e az \$\alpha$\ paraméter értéke úgy, hogy az alábbi függvény egy ξ valószínűségi változó sűrűségfüggvénye legyen? Ha igen, adja meg az \$\alpha$\ paraméter értékét és számítsa ki a valószínűségi változó várható értékét!

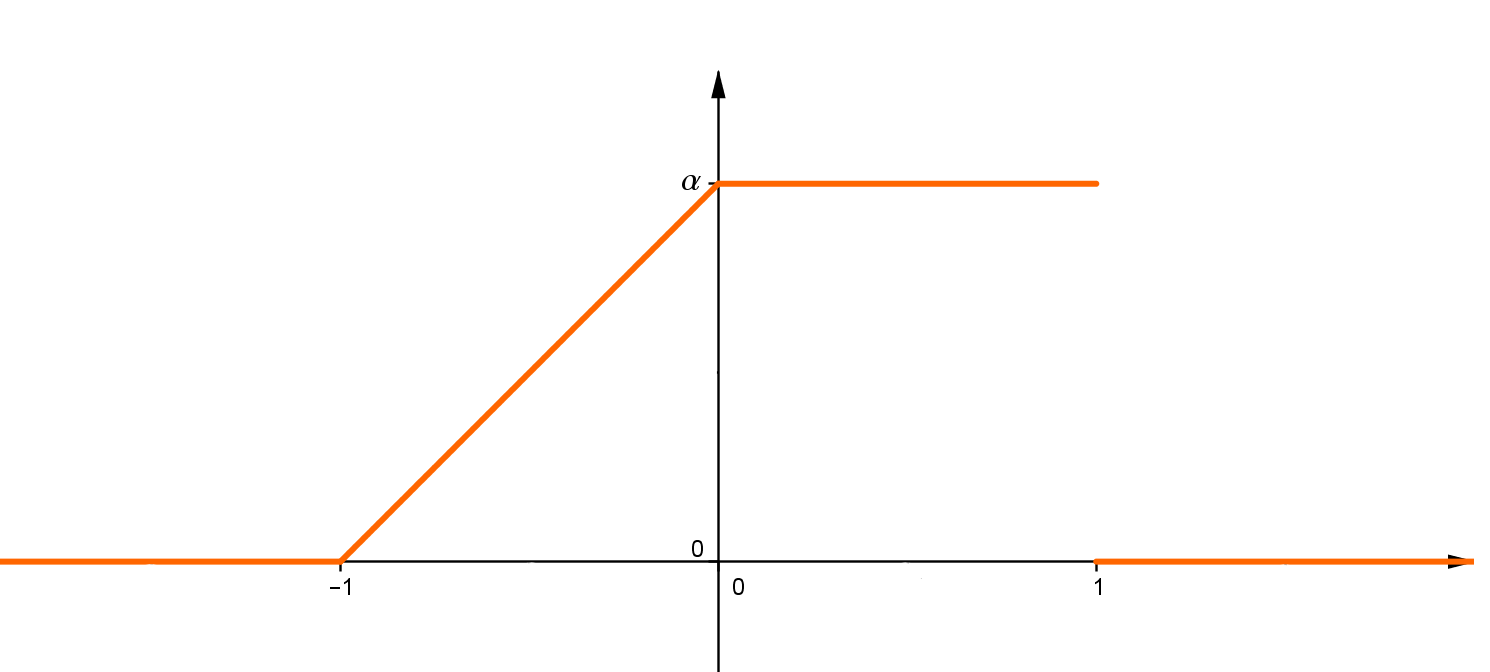
Ehhez a feladathoz azt kell tudni, hogy a sűrűségfggvény integrálja -∞-től ∞-ig 1, azaz a grafikonon a vonal alatti terület 1. Ezen az ábrán nagyon könnyen kiszámolható a terület, mert ez egy trapéz:

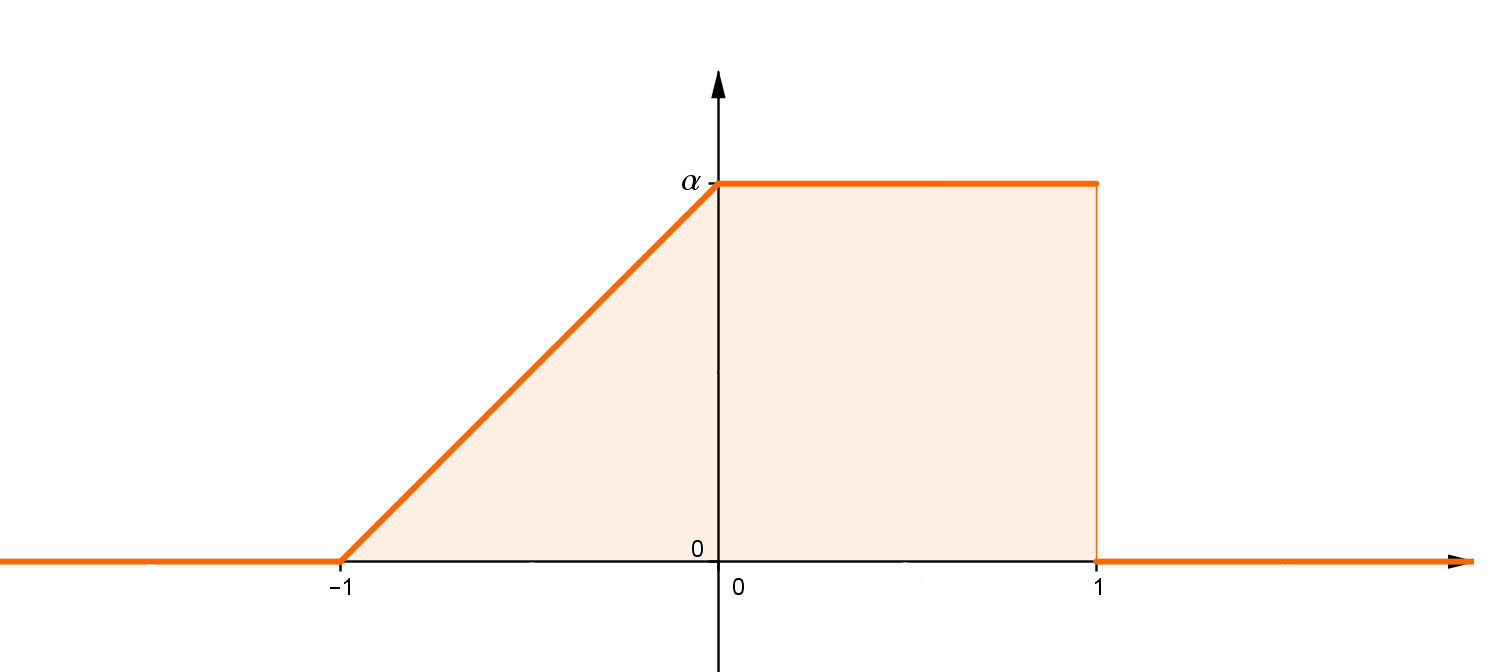
A trapéz területére van képlet:
$$ T=\frac{a+c}{2}\cdot m $$ Az a és a c a trapéz alja és teteje, m a magassága. A rajz alapján: a = 2, c = 1, m = \$\alpha$\, aterületnek pedig ugye 1-nek kell lennie, T = 1. Ezeket helyettesítsük be a képletbe:
$$ 1=\frac{2+1}{2}\cdot \alpha $$ Ebből kiszámíthatjuk \$\alpha$\-t: \$\alpha=\frac 23$\.

Azért csináljuk meg integrálással is, ahogy illik, mert más esetben nem ilyen könnyű kiszámolni a területet. Tehát -∞-től ∞-ig kell integrálni. Mivel a függvény -1-nél kisebb és 1-nél nagyobb számokra 0, az integrálást -1-től 1-ig végezzük el. viszont a függvénynek 0-ban törése van, ezért kettészedjük -1-től 0-ig és 0-tól 1-ig integrálra. Az első szakasz egy egyenes, ami \$\alpha$\-ban metszi az x-tengelyt, és a meredekség is \$\alpha$\, mert amikor 1-et megyünk az x-tengelyen jobbra, akkor \$\alpha$\-t megyünk az y-tengelyen felfelé. Tehát az egyenes:

\$ f(x)=\alpha \cdot x + \alpha $\

Ezt kell -1-től 0-ig integrálni:
$$ \int_{-1}^{0} \alpha \cdot x + \alpha \textrm{ d}x = \left[ \alpha \cdot \frac{x^2}{2} + \alpha\cdot x\right]_{-1}^{0}=\frac {\alpha}{2} $$ A második szakasz is egyenes, de vízszintes, ami megfelel egy konstans függvénynek: f(x)=\$\alpha$\. Ezt integráljuk 0-tól 1-ig:
$$ \int_{0}^{1} \alpha \textrm{ d}x = \left[ \alpha\cdot x\right]_{0}^{1}=\alpha $$ A két integrál összege a terület, ennek kell 1-nek lenni:
$$ \frac {\alpha}{2} + \alpha = 1 $$ Ebből \$\alpha=\frac 23$\-ot kapunk ismételten.

Ki kell még számolni a várható értéket. Ezt úgy kapjuk meg, ha a sűrűségfüggvényt szorozzuk x-szel, és ezt integráljuk -∞-től ∞-ig. Ez a képlet biztosan ismerős:
$$ M(\xi) =\int_{-\infty}^{\infty} f(x)\cdot x \textrm{ d}x $$ Most is csak -1-től 1-ig kell integrálni, mert ezen a részen kívül 0. És megint két részletben integrálunk, előbb -1-től 0-ig:
$$ \int_{-1}^{0} \left(\frac 23 \cdot x + \frac 23 \right)\cdot x \textrm{ d}x = \int_{-1}^{0} \frac 23 \cdot x^2 + \frac 23 \cdot x \textrm{ d}x = $$ $$ = \left[ \frac 23 \cdot \frac{x^3}{3} + \frac 23 \cdot \frac{x^2}{2}\right]_{-1}^{0}=-\frac 19 $$ A \$\frac 23$\-ok úgy kerültek be, hogy \$\alpha$\ helyett ezt írtam. Számoljuk kia második szakaszra is:
$$ \int_{0}^{1} \frac 23 \cdot x \textrm{ d}x = \left[ \frac 23 \cdot \frac{x^2}{2}\right]_{0}^{1}=\frac 13 $$ Ezt a két integrálértéket kell összeadni: \$-\frac 19 + \frac 13 = \frac 29$\. Tehát a várható érték \$ M(\xi)=\frac 29$\.

3. A Cseresznyejáték Zrt. által forgalmazott Mákospatkó nevű sorsjegy 200 Ft-ba kerül. 1 millió szelvényt hoznak forgalomba, melyek közül az alábbi táblázat szerint oszlik meg a nyeremény:

Szelvények száma	Nyeremény
2 db	5 000 000 Ft
500 db	50 000 Ft
30 000 db	1 000 Ft
400 000 db	200 Ft

Ha egy szelvényt vásárolunk, várhatóan mennyit nyerünk?

Ezt a feladatot diszkrét eloszlással oldhatjuk meg, mert akármilyen érték nem lehet, csak az a néhány, ami a táblázatban van. Illetve a táblázatot kicsit módosítani kell, mert a nettó nyeremény a nyeremény mínusz a sorsjegy ára. És a táblázatból az is hiányzik, hogy nem nyerünk semmit (vagyis lényegében veszítünk 200 Ft-ot). A másik, amit meg kell változtatni, az a szelvények száma. Ehelyett ugyanis a valószínűséget kell írni, ami a nyertes szelvény aránya az összes szelvényhez képest. (Mert ugye valószínűséget úgy számolunk, hogy kedvezőperösszes.)

Az új táblázat:

xi	pi
4 999 800	\$ \frac{2}{1 000 000} $\
49 800	\$ \frac{500}{1 000 000} $\
800	\$ \frac{30 000}{1 000 000} $\
0	\$ \frac{400 000}{1 000 000} $\
-200	\$ \frac{569498}{1 000 000} $\

Az első oszlopba úgy jöttek ki a számok, hogy a nyereményekből levontam 200-at, és még az utolsó sorba került -200, ami a nem nyertes szelvénynek felel meg. A második oszlopba pedig a nyertes szelvények számát osztottam az összes szelvény számával, 1 millióval.

Most lehet a várható értéket kiszámolni. Diszkrét eloszlásnál így kell:
$$ M(\xi)=\sum_{i=1}^{n} x_i p_i = x_1 p_1 + x_2 p_2 + ... + x_5 p_5 $$
Helyettesítsük be a táblázat értékeit:
$$ M(\xi)=4999800 \cdot \frac{2}{1 000 000} + 49800 \cdot \frac{500}{1 000 000} + $$

$$ + 800 \cdot \frac{30 000}{1 000 000}+ 0 \cdot \frac{400 000}{1 000 000}+ (-200) \cdot \frac{569498}{1 000 000} = -55 $$
Tehát várhatóan -55 Ft-ot nyerünk, vagyis nem mi, hanem a Cseresznyejáték Zrt. fog jól járni.

Másképpen is megkaphatjuk ezt az eredményt. A Cseresznyejáték Zrt. szelvényenként 200 Ft-ot keres és van 1 millió sorsjegy. Ez összesen 200 millió Ft bevétel. Viszont ki kell fizetnie 2-szer 5 millió, 500-szor 50 000 stb Ft-ot, összesen 145 000 000 Ft-ot. A nettó bevétele tehát 200 000 000 - 145 000 000 = 55 000 000 Ft. Ezt leosztva 1 millióval, megkapjuk, hogy szelvényenként 55 Ft haszna van. Ebből következik, hogy a játékosnak 55 Ft vesztesége van.