Hogyan oldjunk meg matek érettségit?

Nézzük meg a 2017-es matek középszintű érettségi megoldását!

I. rész

1. Egy 27 fős osztályban mindenki tesz érettségi vizsgát angolból vagy németből. 23 diák vizsgázik angolból, 12 pedig németből.
Hány olyan diák van az osztályban, aki angolból és németből is tesz érettségi vizsgát?

Ha az összes diákból kivonjuk az angolból vizsgázókat, akkor a csak németből vizsgázókat kapjuk meg: $$ \textrm{Csak németből: }27-23=\color{green}{4} $$ Ugyanígy, ha az összes diákból kivonjuk a németből vizsgázókat, akkor a csak angolból vizsgázókat kapjuk meg: $$ \textrm{Csak angolból: }27-12=\color{green}{15} $$ Tehát van 4 tanuló, aki csak németből, 15 tanuló, aki csak angolból, a többi pedig mindkét nyelvből érettségizik. Tehát 27 - 4 - 15 = 8 tanuló mindkét nyelvből vizsgázik.

2. Egy mértani sorozat második tagja 6, harmadik tagja -18.
Adja meg a sorozat ötödik tagját!

Mértani sorozatnál a következő tagot úgy kapjuk meg, hogy az előző tagot szorozzuk valamennyivel. A feladatban a 2. tag után a 3. jön, konkrétan 6 után -18. Mennyivel kell szorozni a 6-ot, hogy -18-at kapjunk? -3-mal, tehát a sorozat minden tagját úgy kapjuk meg, hogy -3-mal szorzunk. A feladat az 5. tagot kérdezi. A 3. tagtól csak két lépés az 5. tag. A 4. tagot a harmadikból így kapjuk meg: (-18)·(-3)=54. Az 5. tagot pedig a 4. tagból kapjuk meg: 54· (-3)=-162. Ez tehát az 5. tag: -162.

3. Egy hatfős asztaltársaság tagjai: Anna, Balázs, Cili, Dezső, Egon és Fruzsina. Mindegyikük pontosan három másik személyt ismer a társaságban. Cili ismeri Dezsőt és Egont, Anna pedig nem ismeri sem Balázst, sem Dezsőt.
Szemléltesse gráffal a társaság ismeretségi viszonyait! (Minden ismeretség kölcsönös.)

Kezdjük azzal, hogy C-t összekötjük D-vel és E-vel, hiszen Cili ismeri Dezsőt és Egont.

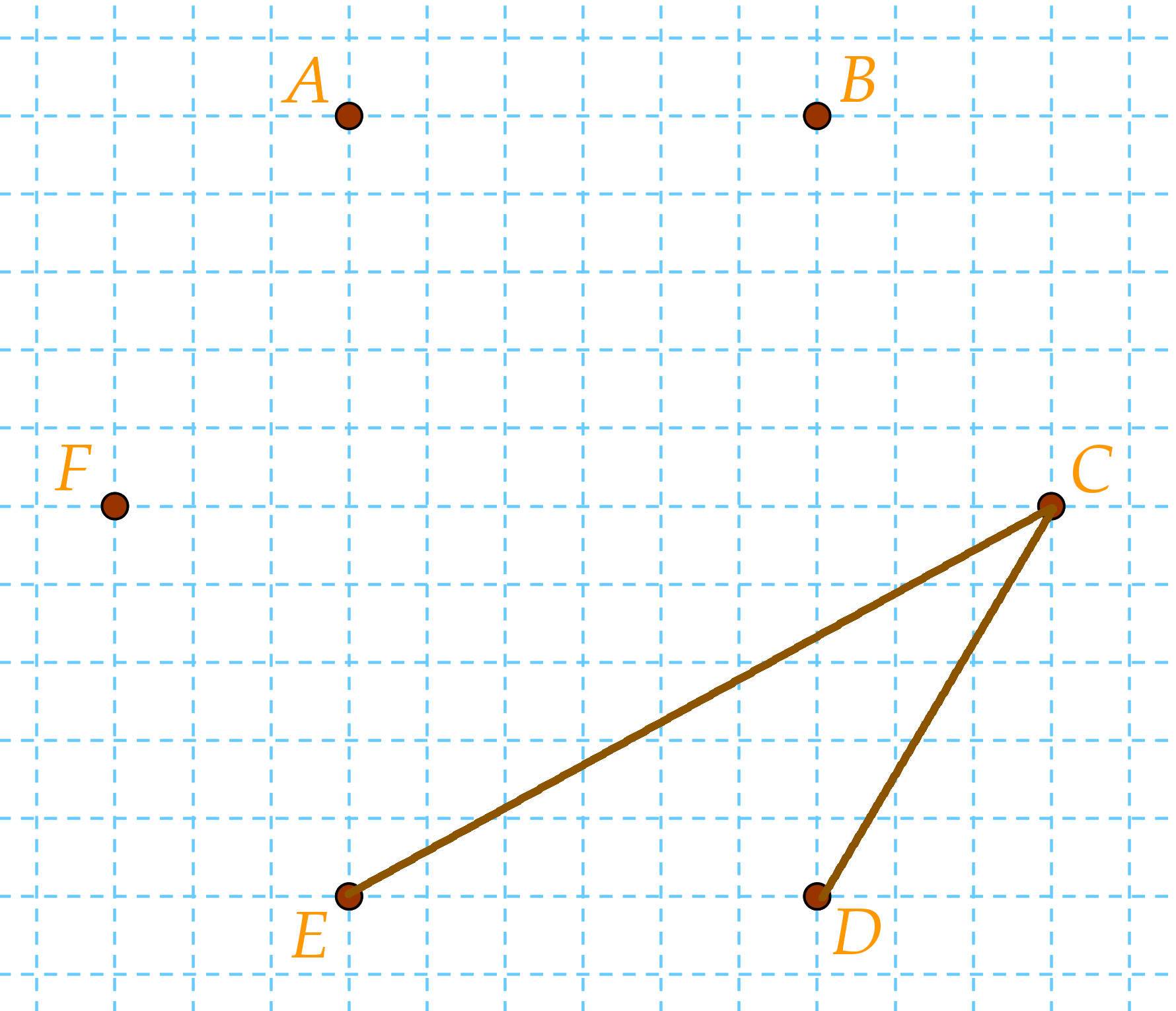
Ezután jön Anna: tudjuk, hogy nem ismeri sem Balázst, sem Dezsőt. De mivel mindenki 3 embert ismer, ezért Annának ismernie kell Cilit, Egont és Fruzsinát. Kössük össze ezért A-t C-vel, E-vel és F-fel.

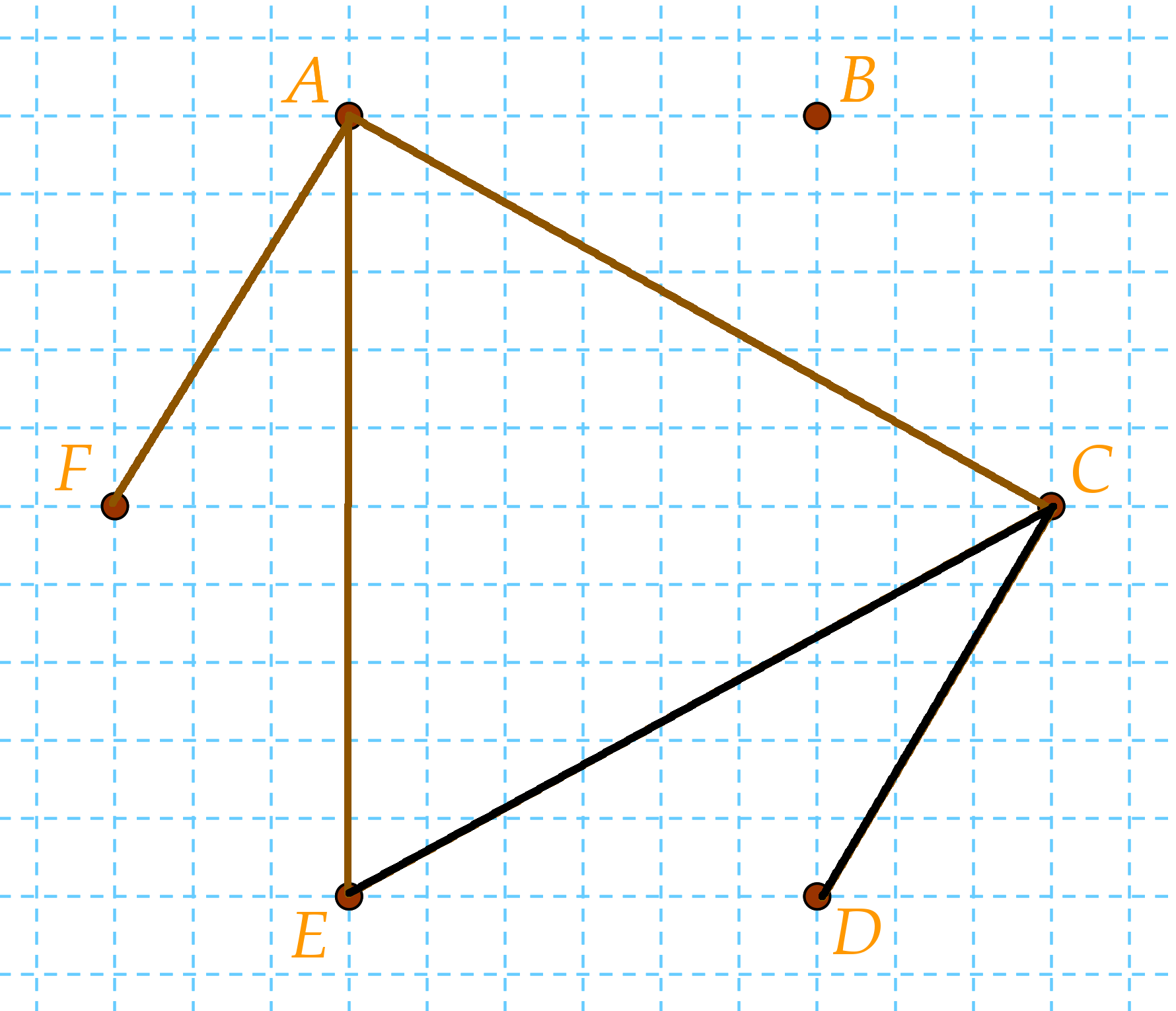
Láthatjuk, hogy most már A-ból és C-ből is 3 vonal megy, tehát oda már nem mehet több vonal. Ezért B-ből csak a D-be, E-be és F-be húzhatunk vonalat.

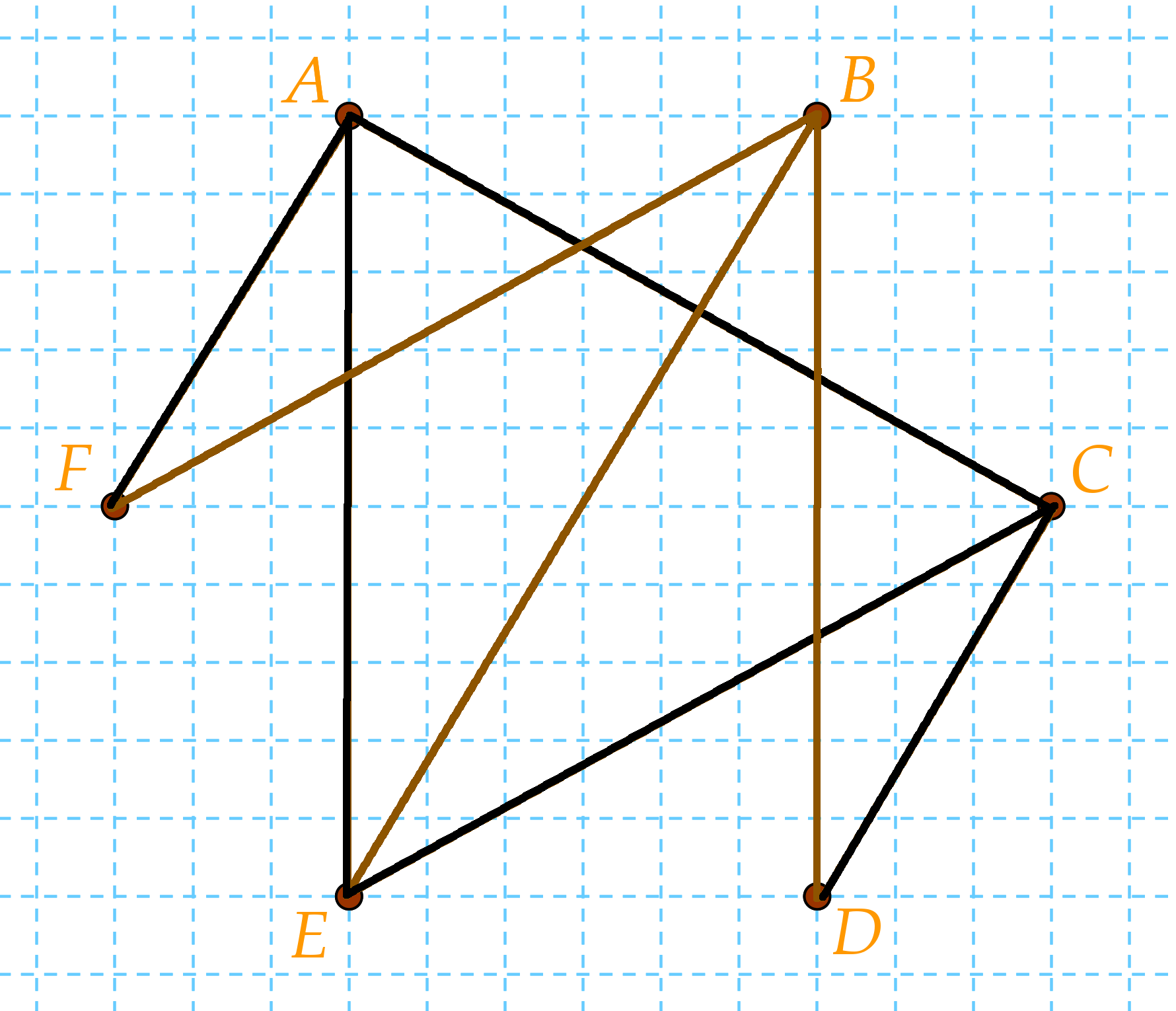
Így már csak a D és az F marad, amiből nem 3 vonal indul ki, ezért kössük össze azokat is, és kész is vagyunk.

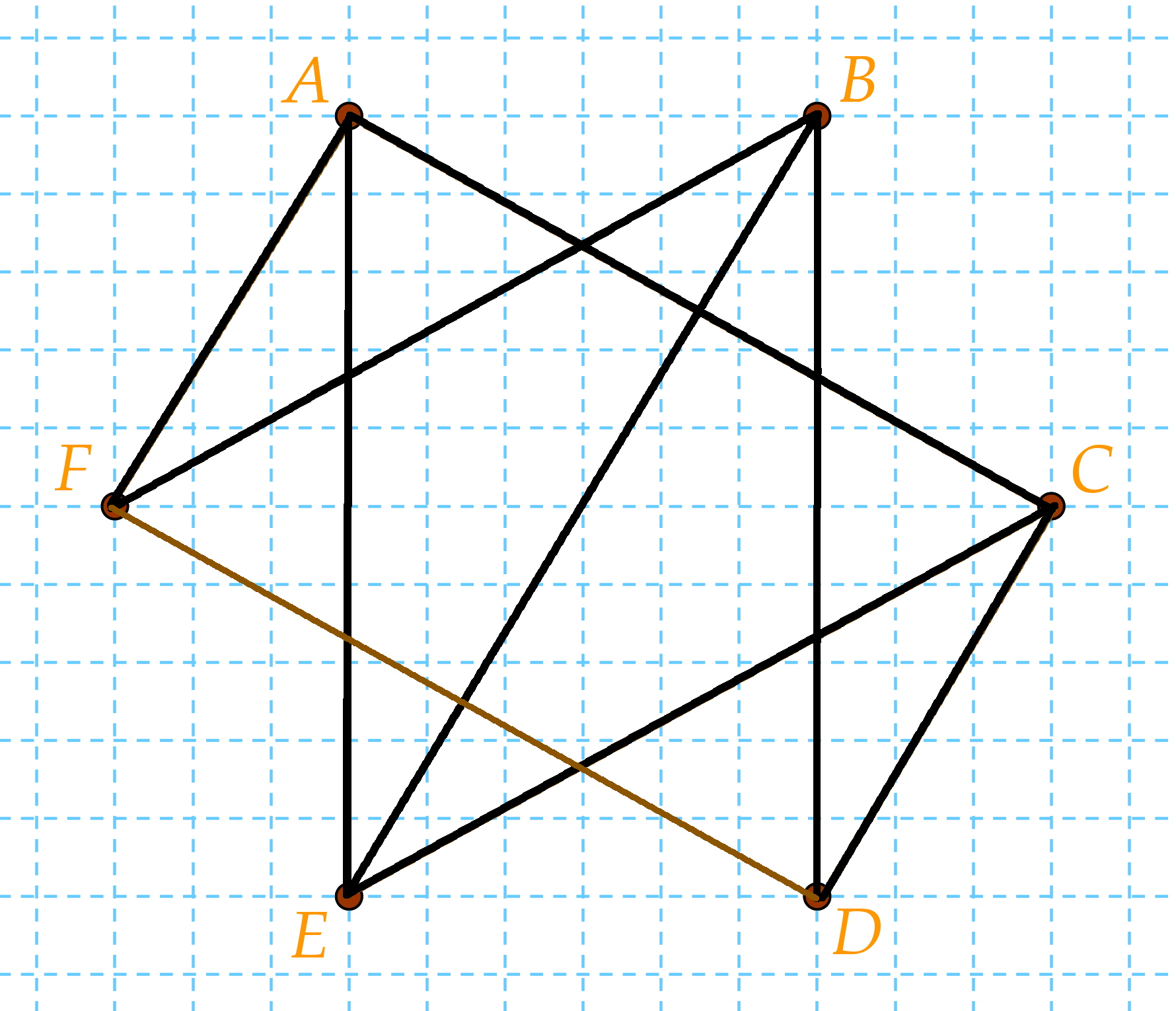
4. Adja meg azt az x valós számot, amelyre log₂x = -3.

Itt azt kell tudni, hogy mi a logaritmus definíciója: $$ \log_{\color{DarkMagenta}{a}}{\color{ForestGreen}{b}}=\color{DarkOrange}{c} \quad \Leftrightarrow \quad \color{DarkMagenta}{a}^{\color{DarkOrange}{c}}=\color{ForestGreen}{b} $$
A feladatban a helyén 2 van, b helyén x és c helyén -3. A szabály alapján alakítsuk át: $$ \log_{\color{DarkMagenta}{2}}{\color{ForestGreen}{x}}=\color{DarkOrange}{-3} \quad \Leftrightarrow \quad \color{DarkMagenta}{2}^{\color{DarkOrange}{-3}}=\color{ForestGreen}{x} $$
Ki kell számolni, mennyi 2^-3. Ezt megtehetjük számológéppel is, ez jön ki: 0,125.

5. Az alábbi hozzárendelési utasítások közül adja meg annak a betűjelét, amely a 0-hoz 4-et, a 2-höz pedig 0-t rendel!

A: x ↦ 2x + 4

B: x ↦ 2x - 4

C: x ↦ -2x + 4

D: x ↦ -2x - 4

Itt annyi a feladat, hogy behelyettesítünk x helyére először 0-t, aztán 2-t. Ha 4 és 0 lesz az eredmény, akkor az a függvény a megoldás.

A: 2·0 + 4 = 4, 2·2 + 4 = 8 → ez tehát nem jó

B: 2·0 - 4 = -4, 2·2 - 4 = 0 → ez sem jó

C: -2·0 + 4 = 4, -2·2 + 4 = 0 → ez jó, tehát a helyes válasz C.

6. Egy háromszög 3 cm és 5 cm hosszú oldalai 60°-os szöget zárnak be egymással. Hány centiméter hosszú a háromszög harmadik oldala? Megoldását részletezze!

Legkönnyebben koszinusz-tétellel tudjuk kiszámolni. $$ \color{DarkMagenta}{c}^2=\color{ForestGreen}{a}^2+\color{DarkOrange}{b}^2-2\color{ForestGreen}{a}\color{DarkOrange}{b}\cos \color{FireBrick}{\gamma} $$

Meg van adva a, b és γ: a = 3 cm, b = 5 cm, γ = 60°. Ezeket helyettesítsük be a képletbe:
$$ \color{DarkMagenta}{c}^2=\color{ForestGreen}{3}^2+\color{DarkOrange}{5}^2-2\cdot\color{ForestGreen}{3}\cdot\color{DarkOrange}{5}\cdot\cos \color{FireBrick}{60} $$ $$ \color{DarkMagenta}{c}^2=9+25-30\cdot0,5 $$ $$ \color{DarkMagenta}{c}^2=34-15 $$ $$ \color{DarkMagenta}{c}^2=19 \qquad /\sqrt{} $$ $$ \color{DarkMagenta}{c}=\sqrt{19}\approx 4,36 $$

Tehát a harmadik oldal 4,36 cm.

7. Egy dobozban lévő színes golyókról szól az alábbi állítás:

„A dobozban van olyan golyó, amelyik kék színű.”

Válassza ki az alábbiak közül az összes állítást, amely tagadása a fentinek!

• A: A dobozban van olyan golyó, amelyik nem kék színű.
• B: A dobozban minden golyó kék színű.
• C: A dobozban egyik golyó sem kék színű.
• D: A dobozban nincs olyan golyó, amelyik kék színű.

Matekban a „van olyan” típusú állításokat kétféleképpen tagadhatjuk: a „van olyan” helyett azt írjuk, hogy „minden”, a mondat második részét pedig tagadjuk. Így a feladat mondatából ez lesz: „A dobozban minden golyó nem kék színű.”. Ez annyira nem értelmes nyelvtanilag, inkább így lenne jó: „A dobozban egyik golyó sem kék színű.” Ez viszont a C válasszal egyezik meg.

A másik tagadási lehetőség, hogy a „van olyan”-t kicsréljük „nincs olyan”-ra, a többi rész változatlan marad: „A dobozban nincs olyan golyó, amelyik kék színű.”. Ez pedig a D válasz. Tehát a két megoldás: C és D.

8. Az alábbi ábrán a [-3; 2] intervallumon értelmezett x ↦ -2·|x - 1| + 3 függvény grafikonja látható.
Adja meg a függvény értékkészletét!

Az értékkészletet az y tengelyen kell nézni. Az ábrán az y tengely szinezett része az értékkészlet.

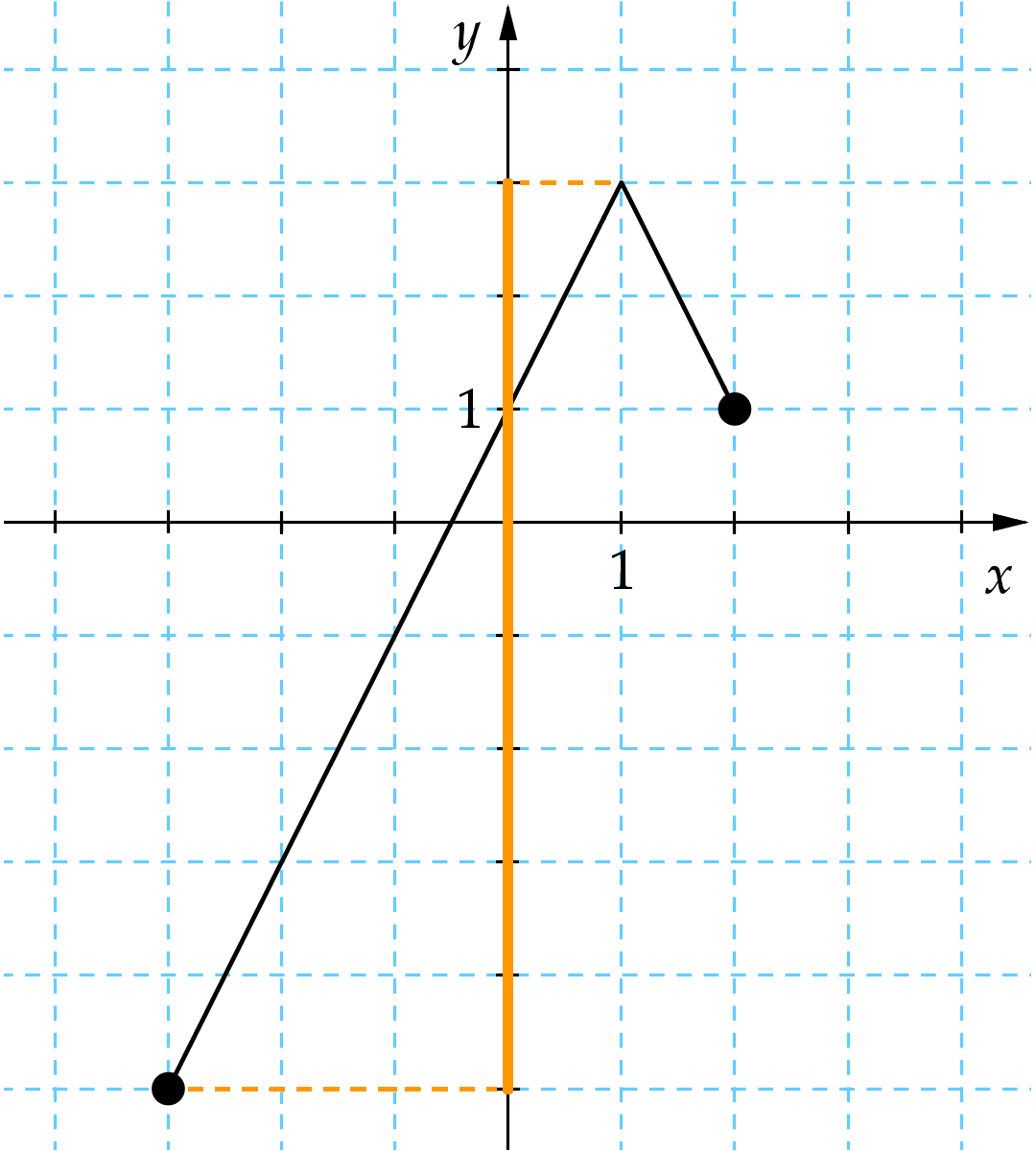
Így már leolvashatjuk, hogy -5 és 3 közötti értékeket vesz vel a függvény, vagyis az értékkészlete: [-5; 3].

9. A Bocitej Kft. 1 literes tejesdobozának alakja négyzet alapú egyenes hasáb. A dobozt színültig töltik tejjel.

Hány cm magas a doboz, ha az alapnégyzet oldala 7 cm? Megoldását részletezze!

A hasáb térfogata: alapterület × magasság. $$ V=T\cdot m $$ Az alapterület egy 7 cm oldalú négyzet területe: T = 7·7 = 49 cm². Ezt kell még megszorozni annyival, hogy 1 litert kapjunk. 1 l = 1000 cm³. $$ 1000=49\cdot m \quad /:49 $$ $$ 20,4= m $$ Tehát a doboz magassága 20,4 cm.

10. Oldja meg az alábbi egyenletet a [0; 2π] intervallumon!
$$ \cos x = 0,5 $$

A legkönnyebben úgy oldhatjuk meg a feladatot, hogy kinyitjuk a függvénytáblázatot a koszinusz függvénynél:

Ezután húzunk egy vízszintes vonalat, ami az y tengelyt a 0,5 pontban metszi. Ez az egyenes a koszinusz grafikonját több pontban is elmetszi. Nekünk azok a pontok kellenek, amik beleesnek a [0; 2π] intervallumba.

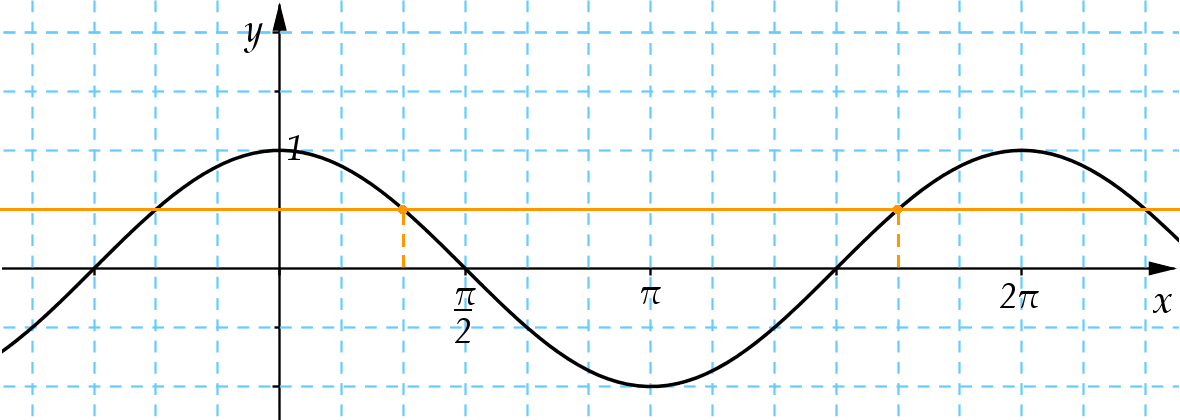
Két ilyen pont van. Az elsőnek az értékét számológéppel megkapjuk: „shift cos” 0,5 = 60°, ami radiánban \$\mathbf{\frac{\pi}{3}}$\. A másik megoldás pedig 2π -\$\frac{\pi}{3}$\ = \$\mathbf{\frac{5\pi}{3}}$\.

11. Ábrázolja az alábbi számegyenesen az |x|<3 egyenlőtlenség valós megoldásait!

Általános iskolában úgy tanították az abszolút értéket, hogy 0-tól való távolság. A feladat tehát az, hogy bejelöljük azokat a számokat, amik a 0-hoz közelebb vannak, mint a 3. Ezek a számok pedig a -3 és a 3 közé eső számok. Mivel nincs megengedve egyenlőség, ezért a -3-hoz és a 3-hoz üres karikát teszünk.

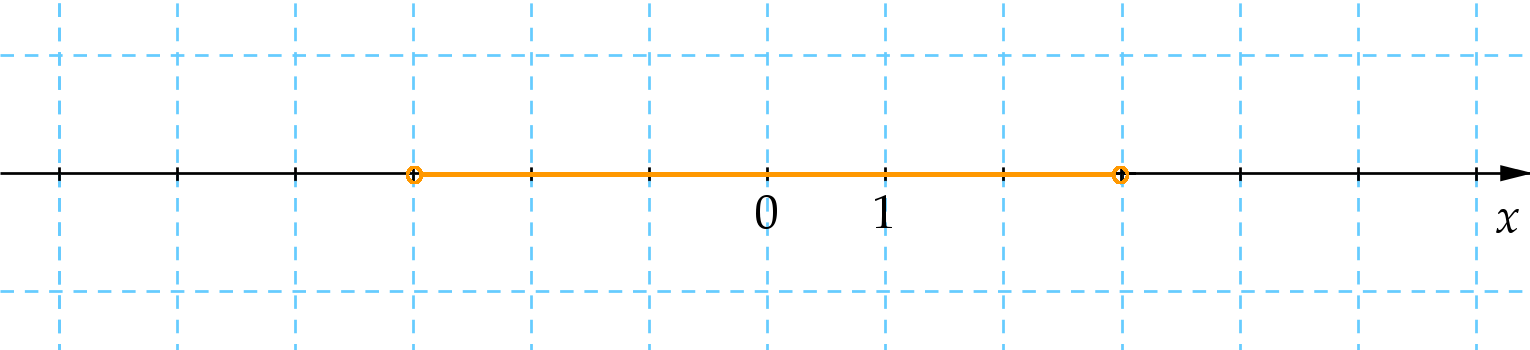
12. Egy kockával kétszer egymás után dobunk.

Adja meg annak a valószínűségét, hogy a két dobott szám összege 7 lesz! Válaszát indo- kolja!

Tudjuk, hogy a valószínűséghez a kedvezőperösszes képletet kell használni. Az összes eset 36, mert az első dobás 6 féle lehet, a második dobás szintén 6 féle lehet, ezért 6·6 = 36.

A kedvező esetek számához azt kell megnézni, hányféleképpen jöhet ki a dobott számok összegére 7. Ezek lehetnek: 1 + 6 = 6 + 1 = 2 + 5 = 5 + 2 = 3 + 4 = 4 + 3, ez összesen 6 lehetőség, tehát ennyi a kedvező esetek száma. A valószínűség: \$\frac{6}{36}=\mathbf{\frac{1}{6}}$\.

II. rész

A

13. Adott a valós számok halmazán értelmezett f függvény: $$ f: x \mapsto (x-1)^2 -4 $$

• a) Számítsa ki az f függvény x = -5 helyen felvett helyettesítési értékét!
• b) Ábrázolja az f függvényt, és adja meg szélsőértékének helyét és értékét!
• c) Oldja meg a következő egyenletet a valós számok halmazán:

$$ (x-1)^2 -4 = -x-1 $$

a) Nagyon egyszerű dolgunk van: csak x helyére -5-öt kell írni, és kiszámolni: (-5-1)² - 4 = (-6)² - 4 = 36 - 4 = 32.

b) Ha függvényábrázolásnál biztosra akarunk menni, akkor csináljunk táblázatot, amiben az első sorban x értékei vannak, alatta pedig a helyettesítési érték (amit úgy számolunk ki, mint az a) részben).

x	-3	-2	-1	0	1	2	3
f(x)	12	5	0	-3	-4	-3	0

Ezeket a pontokat berajzoljuk a koordináta-rendszerbe és összekötjük.

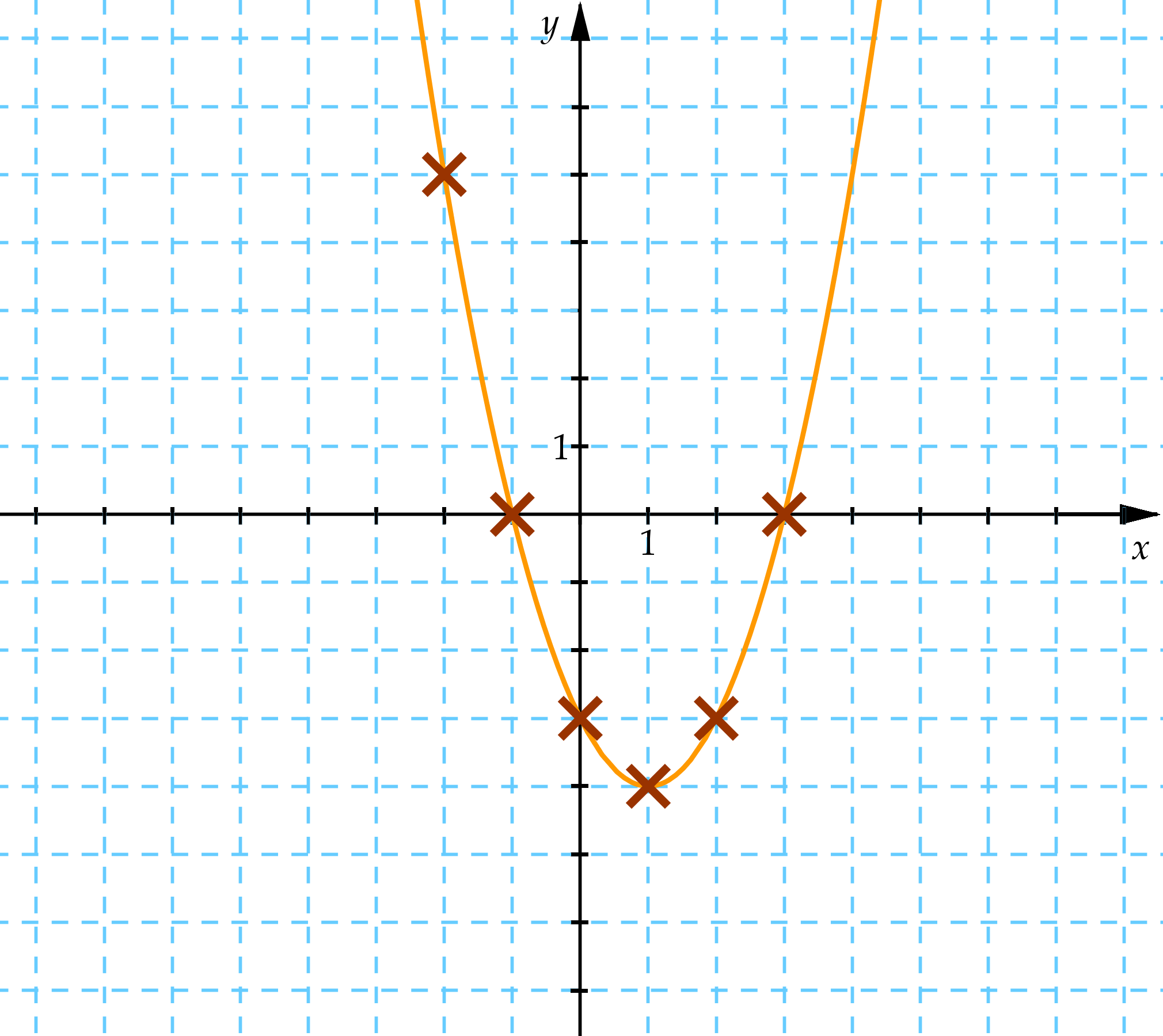
Az ábra alapján a szélsőértéket is le tudjuk olvasni:

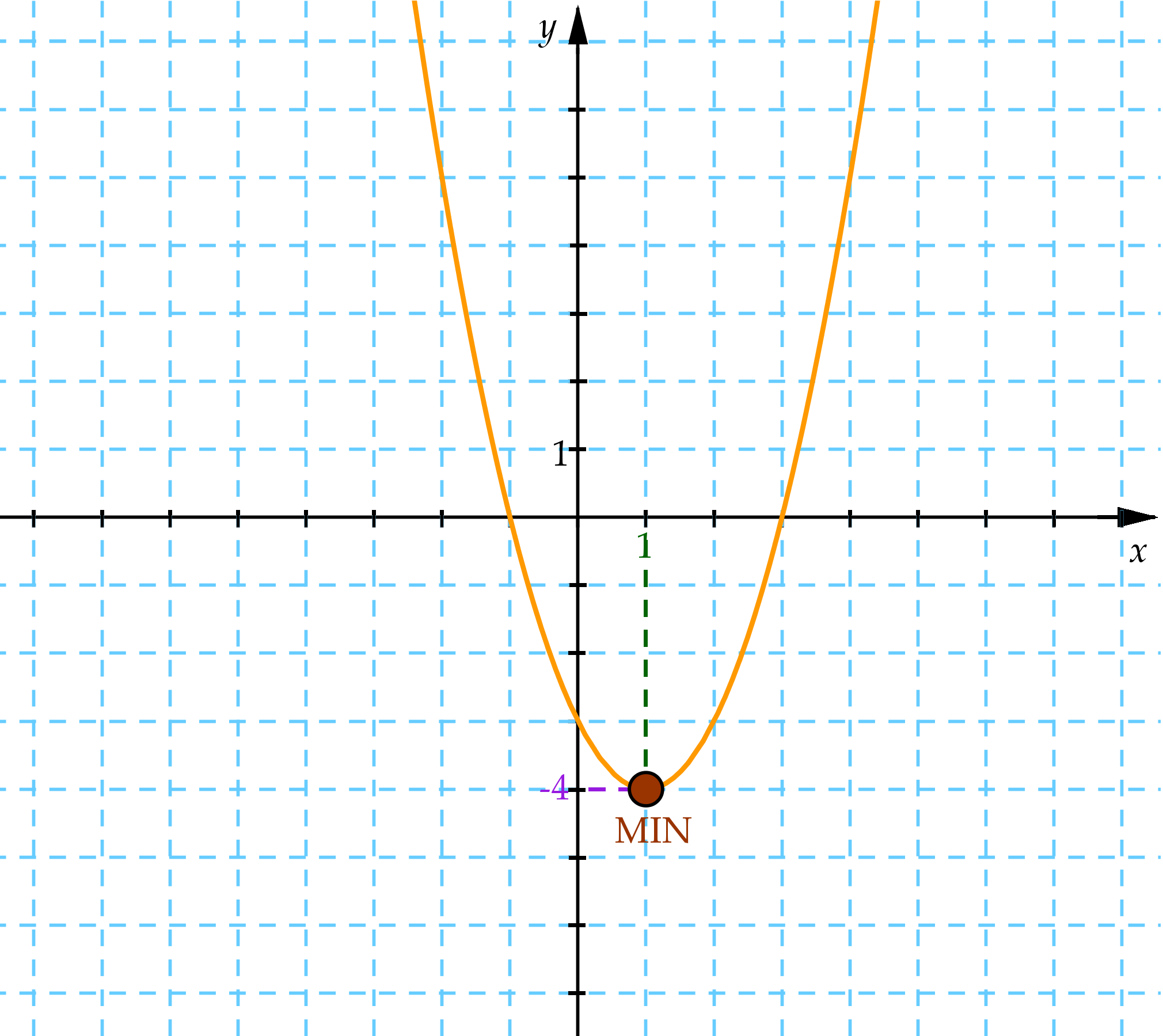
Tehát a minimum hely: x = 1, minimum érték: y = -4.

c) Az egyenletet oldjuk meg simán zárójelfelbontással, átrendezéssel stb. $$ (x-1)^2 -4 = -x-1 \qquad /\textrm{zárójelfelbontás} $$ $$ x^2 - 2x + 1 -4 = -x-1 \qquad /\textrm{összevonás} $$ $$ x^2-2x-3 = -x-1 \qquad /+x, \ +1 $$ $$ x^2-x-2 =0 \qquad / \textrm{megoldóképlet} $$ $$ \boldsymbol{x_1=-1}, \ \boldsymbol{x_2=2} $$

Érettségin ne felejts el ellenőrizni!

14. Az ABC derékszögű háromszög egyik befogója 8 cm, átfogója 17 cm hosszú.

• a) Számítsa ki a háromszög 17 cm-es oldalához tartozó magasságának hosszát!
• b) Hány cm² a háromszög körülírt körének területe?



A DEF háromszög hasonló az ABC háromszöghöz, és az átfogója 13,6 cm hosszú.

• c) Hány százaléka a DEF háromszög területe az ABC háromszög területének?

a) Kezdjük azzal, hogy Pitagorsz-tétellel kiszámítjuk a másik befogót.

a = 8 cm, c = 17 cm, b = ?

$$ \color{DarkMagenta}{a}^2+\color{DarkOrange}{b}^2=\color{ForestGreen}{c}^2 $$ $$ \color{DarkMagenta}{8}^2+\color{DarkOrange}{b}^2=\color{ForestGreen}{17}^2 $$ $$ 64+\color{DarkOrange}{b}^2=289 \qquad /-64 $$ $$ \color{DarkOrange}{b}^2=225 \qquad /\sqrt{} $$ $$ \color{DarkOrange}{b}=15 $$

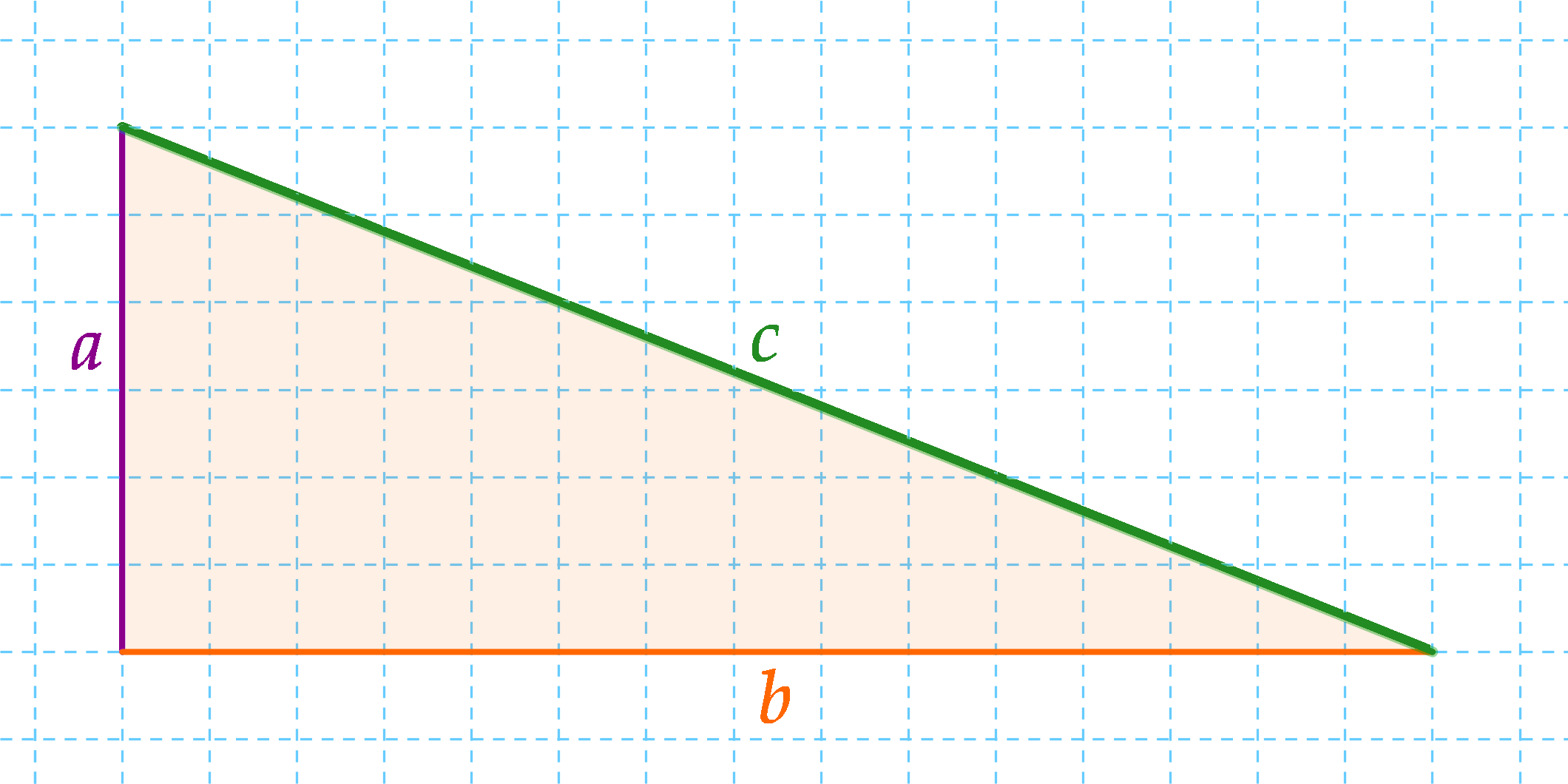
Most már kiszámolhatjuk a magasságot. Egy lehetőség erre a háromszög területének kiszámolása. Egyrészt a derékszögű háromszög egy félbevágott téglalap, aminek a területét egyszerűen az oldalak szorzatával tudjuk kiszámolni: T=a·b. A háromszög területe ennek a fele: T_Δ=\$\frac{a\cdot b}{2}$\. A másik lehetőség, hogy az alapszor magasság per kettő képlettel számolunk: T_Δ=\$\frac{c\cdot m}{2}$\ (itt most az alap nem az a oldal, hanem a c). Rajzoljuk is be a magasságot:

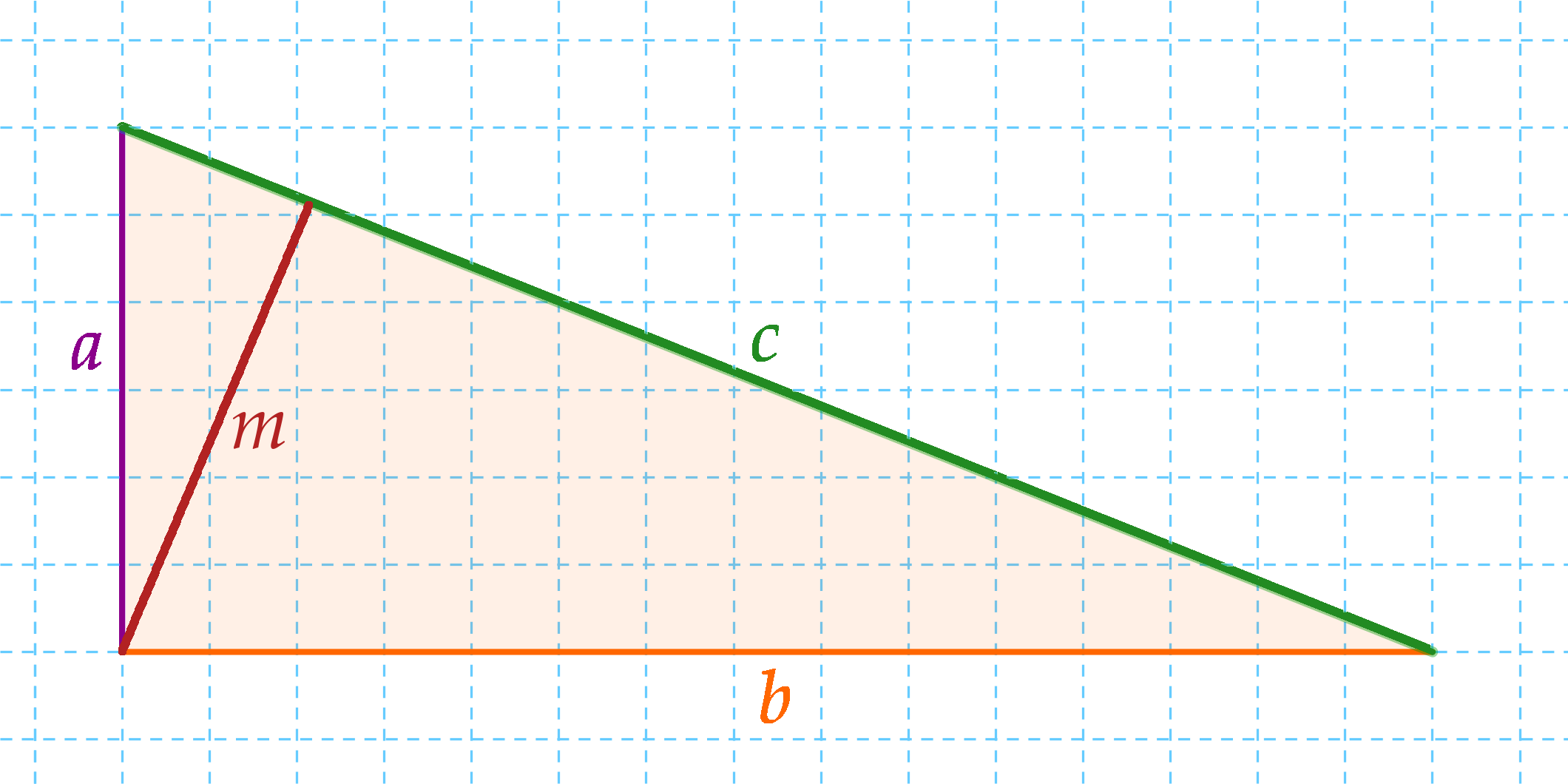
Ha a területet kétféleképpen számoljuk ki, akkor is ugyanannyit kell kapni, ezért a két területképlet egyenlő: $$ \frac{\color{DarkMagenta}{a}\cdot \color{DarkOrange}{b}}{2}=\frac{\color{ForestGreen}{c}\cdot\color{FireBrick}{m}}{2} \quad /\cdot 2 $$ $$ \color{DarkMagenta}{a}\cdot \color{DarkOrange}{b}=\color{ForestGreen}{c}\cdot\color{FireBrick}{m} $$

Helyettesítsük be a számokat: $$ \color{DarkMagenta}{8}\cdot \color{DarkOrange}{15}=\color{ForestGreen}{17}\cdot\color{FireBrick}{m} $$ $$ 120=\color{ForestGreen}{17}\cdot\color{FireBrick}{m} \quad /:17 $$ $$ \color{FireBrick}{m} = \mathbf{7,06 \ cm} $$

b) Derékszögű háromszögnél a körülírt kör középpontja az átfogó felezőpontja. Ebből következik, hogy az átfogó a kör átmérője is egyben. Annak fele pedig a sugár. Tehát: r = \$\frac{17}{2}$\ = 8,5 cm. Innen már csak egy lépés a kör területét kiszámolni, egyszerű képletbehelyettesítés: T_ο = r²π = 8,5²·π = 226,98 cm².

c)A kérdés az, hogy az ABC háromszög területének hány %-a a DEF háromszög területe: $$ T_{ABC}\cdot \color{ForestGreen}{? \%} = T_{DEF} \quad /:T_{ABC} $$ $$ \color{ForestGreen}{? \%} = \color{FireBrick}{\frac{T_{DEF}}{T_{ABC}}} $$

Lehetne azt csinálni, hogy kiszámoljuk a hasonlósági arány ismeretében a többi oldalt és a területeket, de van egyszerűbb megoldás. A területek aránya megegyezik az oldalak arányának négyzetével: $$ \frac{T_1}{T_2}=\left(\frac{a_1}{a_2}\right)^2=\left(\frac{b_1}{b_2}\right)^2=\left(\frac{c_1}{c_2}\right)^2 $$

Ha a T₁ = T_DEF és T₂ = T_ABC, akkor a területek arányát nagyon könnyen ki tudjuk számolni: $$ \frac{T_1}{T_2}=\color{FireBrick}{\frac{T_{DEF}}{T_{ABC}}} =\left(\frac{c_1}{c_2}\right)^2=\left(\frac{13,6}{17}\right)^2=0,8^2= \color{ForestGreen}{0,64} $$ Így már látszik, hogy a megoldás 64%.

15. Az alábbi kördiagram egy balatoni strandon a júliusban megvásárolt belépőjegyek típusának eloszlását mutatja.

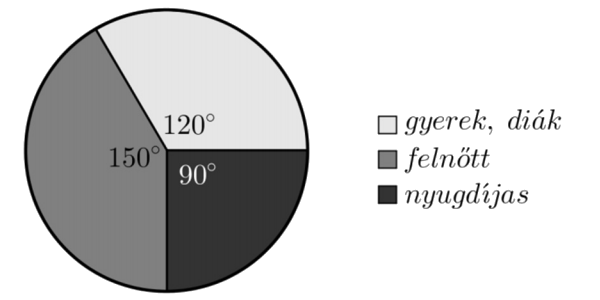
Júliusban összesen 16 416 fő vásárolt belépőjegyet. A belépőjegyek árát az alábbi táblázat tartalmazza.

gyerek, diák	350 Ft/fő
felnőtt	700 Ft/fő
nyugdíjas	400 Ft/fő

• a) Mennyi volt a strand bevétele a júliusban eladott belépőkből?



A tapasztalatok szerint júliusban folyamatosan nő a strandolók száma. Ezért a strandbüfében bevált rendszer, hogy a július 1-jei megrendelést követően július 2-től kezdve július 31-ig minden nap ugyanannyi literrel növelik a nagykereskedésből megrendelt üdítő mennyiségét.

A könyvelésből kiderült, hogy július 1-jén, 2-án és 3-án összesen 165 litert, július 15-én pedig 198 litert rendeltek.

• b) Hány liter üdítőt rendeltek júliusban összesen?

a) Számoljuk ki, melyik fajta jegyből mennyit vettek. Ezt a kördiagram szögeinek arányából tudjuk kiszámolni: nyugdíjas : gyerek : felnőt = 90 : 120 : 150 = 3 : 4 : 5. Ha arányok vannak megadva, akkor legkönnyebben úgy számolhatunk, ha az arányszámokhoz hozzáírunk egy x-et: 3x : 4x : 5x. Ez azt jelenti, hogy nyugdíjas jegyből 3x-et, gyerek jegyből 4x-et, felnőtt jegyből pedig 5x-et adtak el. Ezek összege:
3x + 4x + 5x = 16416
12x = 16416
x = 1368

Ezek alapján az eladott jegyek száma:

• nyugdíjas: 3x = 3·1368 = 4104
• gyerek: 4x = 4·1368 = 5472
• felnőtt: 5x = 5·1368 = 6840

És a jegyekből származó bevétel:

• nyugdíjas: 4104·400 Ft = 1 641 600 Ft
• gyerek: 5472·350 Ft = 1 915 200 Ft
• felnőtt: 6840·700 Ft = 4 788 000 Ft

Ez pedig összesen: 1 641 600 Ft + 1 915 200 Ft + 4 788 000 Ft = 8 344 800 Ft.

b. Az talán nyilvánvaló, hogy számtani sorozattal kell számolni. Amit tudunk: az első három napon összesen 165 litert rendeltek. Ez azt jelenti, hogy a sorozat első három tagjának összege 165: $$ a_1 + a_2 + a_3 = 165 \qquad (1) $$ A másik, amit tudunk, hogy 15-én 198 litert rendeltek, azaz tudjuk a sorozat 15. tagját: $$ a_{15} = 198 \qquad (2) $$ A számtani sorozat n . tagjára van egy képlet: $$ a_ \color{DarkMagenta}{n} = \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + ( \color{DarkMagenta}{n}-1)\cdot \color{DarkOrange}{d} $$ Az (1) és (2) egyenletekben a₁ -et, a₂-t, a₃-at és a₁₅-öt írjuk át az a_n képlet szerint: $$ \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + \color{DarkOrange}{d} + \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + 2\color{DarkOrange}{d} = 165 \qquad (3) $$ $$ \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + 14\color{DarkOrange}{d} = 198 \qquad (4) $$ A (3) egyenletben össze lehet vonni, a (4) egyenletből pedig kifejezhetjük a₁ -et: $$ 3\color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + 3\color{DarkOrange}{d} = 165 \qquad (5) $$ $$ \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} = 198 -14\color{DarkOrange}{d} \qquad (6) $$ Az (5) egyenletet még osszuk le 3-mal, utána helyettesítsük be a₁ helyére a 198 - 14d -t: $$ 3\color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + 3\color{DarkOrange}{d} = 165 \qquad /:3 $$ $$ \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + \color{DarkOrange}{d} = 55 \qquad /:3 \qquad (7) $$ $$ 198-14\color{DarkOrange}{d} + \color{DarkOrange}{d} = 55 \qquad (8) $$ $$ 198-13\color{DarkOrange}{d} = 55 \qquad /-198 \qquad (9) $$ $$ -13\color{DarkOrange}{d} = -143 \qquad /:(-13) \qquad (10) $$ $$ \color{DarkOrange}{d} = \color{DarkOrange}{11} \qquad (11) $$ Megkaptuk d -t, ezt visszahelyettesítjük (6)-ba, és megkapjuk a₁ -et: $$ \color{ForestGreen}{a}_{ \color{ForestGreen}{1}} = 198 -14\cdot \color{DarkOrange}{11} = \color{ForestGreen}{44} \qquad (12) $$ Most már csak a júliusban rendelt összmennyiséget kell kiszámolni, amit a sorozat összegképletével tudunk megtenni: $$ S_ \color{DarkMagenta}{n}=\frac{2\color{ForestGreen}{a}_{ \color{ForestGreen}{1}} + ( \color{DarkMagenta}{n}-1)\cdot \color{DarkOrange}{d}}{2}\cdot \color{DarkMagenta}{n} $$ A képletben n helyére 31 -et írunk, mert július 31 napos, d helyére 11 -et, a₁ helyére pedig 44 -et: $$ S_{\color{DarkMagenta}{31}}=\frac{2\cdot \color{ForestGreen}{44} + (\color{DarkMagenta}{31}-1)\cdot \color{DarkOrange}{11}}{2}\cdot \color{DarkMagenta}{31}=6479 $$ Tehát kijött, hogy 6 479 liter üdítőt rendeltek júliusban.

16. Adott két pont a koordinátasíkon: A(2; 6) és B(4; -2).

• a) Írja fel az AB szakasz felezőmerőlegesének egyenletét!
• b) Írja fel az A ponton átmenő, B középpontú kör egyenletét!



Adott az y = 3x egyenletű egyenes és az x² + 8x + y² - 4y = 48 egyenletű kör.

• c) Adja meg koordinátáikkal az egyenes és a kör közös pontjait!

a) Egy egyenes egyenletét kell felírnunk. Ehhez szükség van egy pontra, amin átmegy az egyenes, és egy vektorra, ami vagy párhuzamos az egyenessel, vagy merőleges rá. Mivel egy szakasz felezőmerőlegese kell, ezért az egyenes átmegy a szakasz felezőpontján.

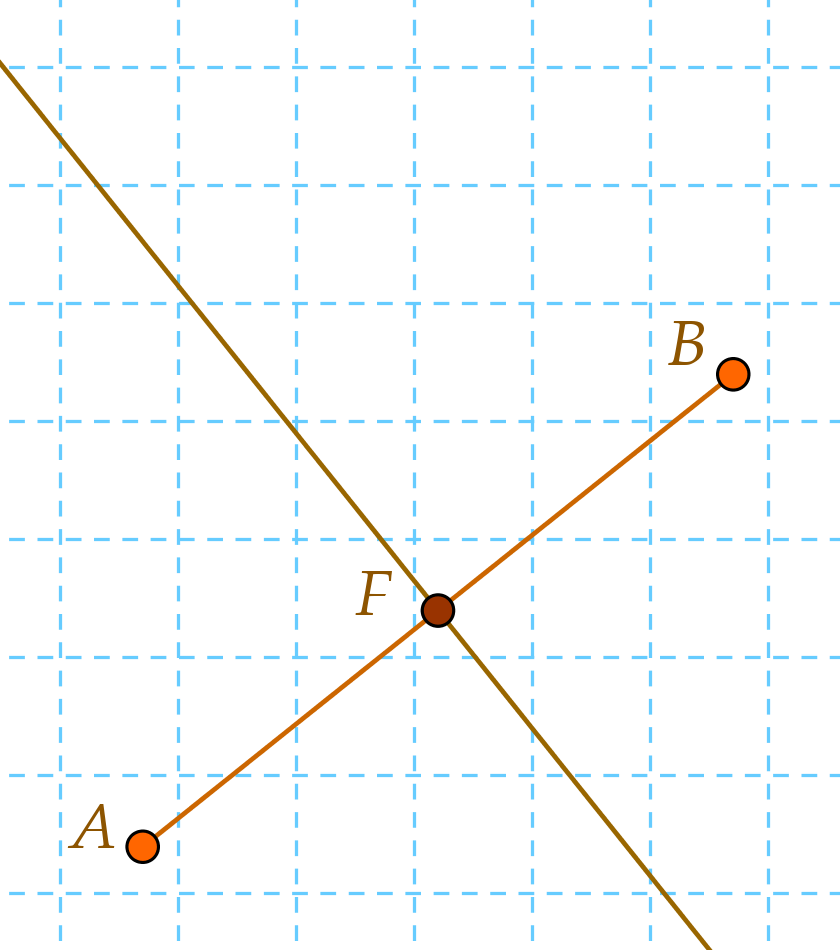
Felezőpontot egyszerűen tudunk számolni, benne van a függvénytáblázatban is: a szakasz végpontjainak a koordinátáit összeadjuk és osztjuk kettővel.

A felezőpont koordinátái: $$ F=\left(\frac{x_1+x_2}{2};\frac{y_1+y_2}{2}\right)=\left(\frac{2+4}{2};\frac{6-2}{2}\right)=(3;2) $$

Ez az F pont lesz az a pont, ami a függvénytáblázatban P₀-val van jelölve az egyenes egyenleténél. Már csak egy vektorra van szükségünk, ami lehet irányvektor vagy normálvektor. Az ábrán az \$\vec{AB}$\ vektor megfelel a célnak, mert merőleges az egyenesre, hiszen felezőmerőlegesről van szó, a normálvektor pedig merőleges az egyenesre.

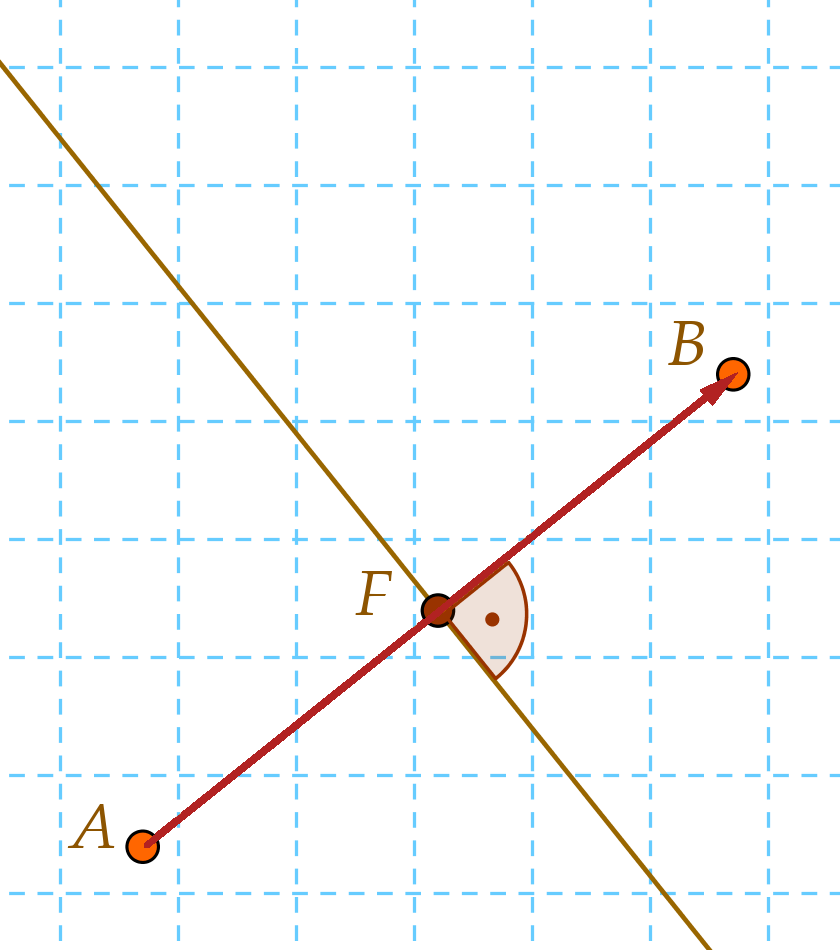
Az \$\vec{AB}$\ vektor koordinátáit fel tudjuk írni, mivel ismerjük a vektor végpontjait, azaz az A és B pontot. Ilyenkor a vektor koordinátáit megkapjuk, ha a vektor végpontjából (B-ből) kivonjuk a kezdőpontját (A-t): $$ \vec{AB}=(4-2;(-2)-6)=(\color{ForestGreen}{2};\color{FireBrick}{-8}) $$

Ez a vektor lesz a normálvektor, amit a függvénytáblázatban n-nel jelölnek, a koordinátái pedig (A ; B ), amit nem szabad összetéveszteni az A és B pontokkal. Tehát a normálvektoros egyenesegyenlet képletében A = 2 és B = -8.

Tehát van egy normálvektorunk: n(2; -8), és van egy pontunk: P₀(3; 2). Ezért az egyenes egyenlete: $$ Ax+By=Ax_0+By_0 $$ $$ 2x+(-8)y=2\cdot 3 + (-8)\cdot 2 $$ $$ \boldsymbol{2x-8y=-10} $$

b) Ha megnézzük a kör egyenletét a függvénytáblázatban, akkor látni, hogy a kör középpontját és a sugarát kell ismerni hozzá:

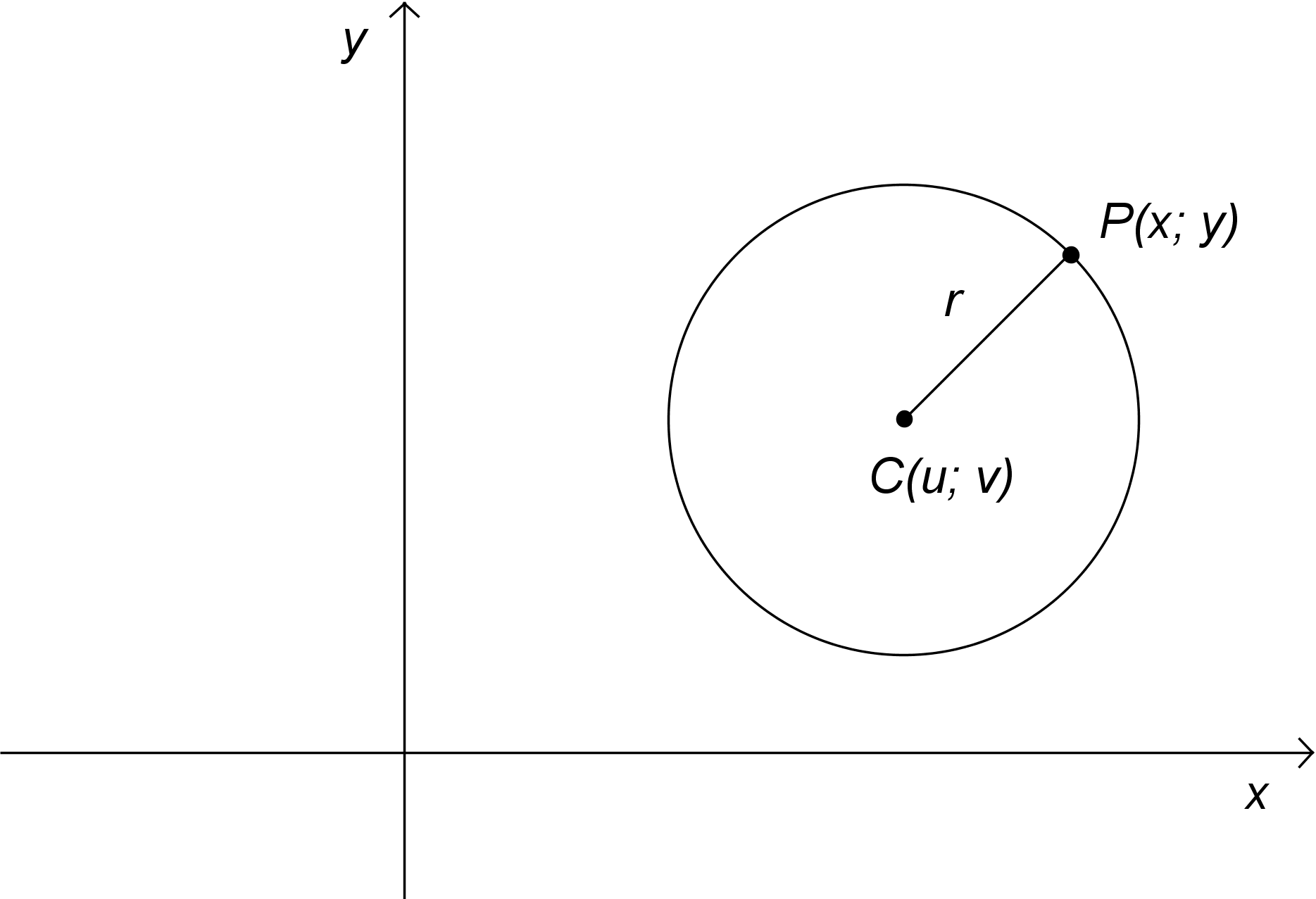
És a kör egyenlete:

$$ (x-u)^2+(y-v)^2 =r^2 $$

A feladat szerint a kör középpontja a B pont, ez a függvénytáblázatban C-vel van jelölve. Mivel a kör átmegy az A ponton, ezért a kör sugarát kiadja az A és B pont távolsága. Két pont távolságára is van egy képlet a függvénytáblázatban, de úgy is kiszámolhatjuk, hogy az \$\vec{AB}$\ vektor hosszát számítjuk ki (az előző feladatban már úgyis megkaptuk az \$\vec{AB}$\ vektort). Egy vektor hosszát úgy számoljuk ki, hogy a koordinátáit négyzetre emeljük, majd összeadjuk, végül gyököt vonunk:

$$ |\vec{AB}|=\sqrt{x^2+y^2}=\sqrt{\color{ForestGreen}{2}^2+(\color{FireBrick}{-8})^2}=\sqrt{4+64}=\sqrt{68} $$

Vagyis megvan a kör sugara: r = \$\sqrt{68}$\. (A gyök ne zavarjon, a kör egyenletében a sugár négyzeten van, ezért a gyök el fog tűnni. Ha mégis zavar, hát ki lehet számolni: \$\sqrt{68}$\ = 8,25.) Most már fel tudjuk írni a kör egyenletét. u és v helyére a B=(4; -2) pont koordinátáit helyettesítjük be, r helyére pedig \$\sqrt{68}$\-at:

$$ (x-4)^2+(y-(-2))^2 =\sqrt{68}^2 $$ $$ \boldsymbol{ (x-4)^2+(y+2)^2 =68} $$

c) Az egyenesnek és a körnek is egyenlete van. Mit csináljunk két egyenlettel? Oldjuk meg egyenletrendszerrel! Mivel az egyenes egyenlete y = 3x , ezért a kör egyenletében y helyére írhatjuk, hogy 3x: $$ x^2+8x+\color{DarkOrange}{y}^2-4\color{DarkOrange}{y} = 48 $$ $$ x^2+8x+(\color{DarkOrange}{3x})^2-4\cdot(\color{DarkOrange}{3x}) = 48 $$ $$ x^2+8x+9x^2-12x = 48 $$ $$ 10 x^2-4x = 48 $$ $$ 10 x^2 -4x - 48 = 0 $$

Amit kaptunk, az egy másodfokú egyenlet, amit könnyű megoldani a megoldóképlettel. A két megoldás: x₁ = -2, x₂ = \$\frac{12}{5}$\ = 2,4. Ha ezeket az értékeket visszahelyettesítjük az y = 3x egyenletbe, megkapjuk y értékeit, vagyis a metszéspontok y koordinátáit: y₁ = 3·x₁ = 3·(-2) = -6 és y₂ = 3·x₂ = 3·2,4 = 7,2. Tehát a két metszéspont: (-2; -6) és (2,4; 7,2).

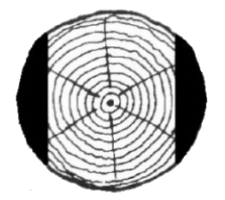17. A Hód Kft. faárutelephelyén rönkfából (henger alakú fatörzsekből) a következő módon készítenek gerendát. A keretfűrészgép először két oldalt levág egy-egy - az ábrán sötéttel jelölt - részt, majd a fa 90°-kal történő elfordítása után egy hasonló vágással végül egy négyzetes hasáb alakú gerendát készít. A gépet úgy állítják be, hogy a kapott hasáb alaplapja a lehető legnagyobb legyen. Most egy forgáshenger alakú, 60 cm átmérőjű, 5 méter hosszú rönkfát fűrészel így a gép.

• a) Igaz-e, hogy a kapott négyzetes hasáb alakú fagerenda térfogata kisebb 1 köbméternél?



A Hód Kft. deszkaárut is gyárt, ehhez a faanyagot 30 000 Ft/m³-es beszerzési áron vásárolja meg a termelőtől. A gyártás közben a megvásárolt fa kb. 40%-ából hulladékfa lesz. A késztermék 1 köbméterét 90 000 forintért adja el a cég, de az eladási ár 35%-át a költségekre kell fordítania (feldolgozás, telephely fenntartása stb.).

• b) Mennyi haszna keletkezik a Hód Kft.-nek 1 köbméter deszkaáru eladásakor?



A fakitermelő cég telephelyéről hat teherautó indul el egymás után. Négy teherautó fenyőfát, kettő pedig tölgyfát szállít.

• c) Számítsa ki annak a valószínűségét, hogy a két, tölgyfát szállító teherautó közvetlenül egymás után gördül ki a telephelyről, ha az autók indulási sorrendje véletlenszerű!

a) A feladatból kiderül, hogy tulajdonképpen egy körből kell négyzetet kivágni. A legnagyobb ilyen négyzetet akkor kapjuk, ha a négyzet minden sarka a körön van. Ennek a négyzetnek az átlója megegyezik a kör átmérőjével, amit megadtak: d = 60 cm = 0,6 m.

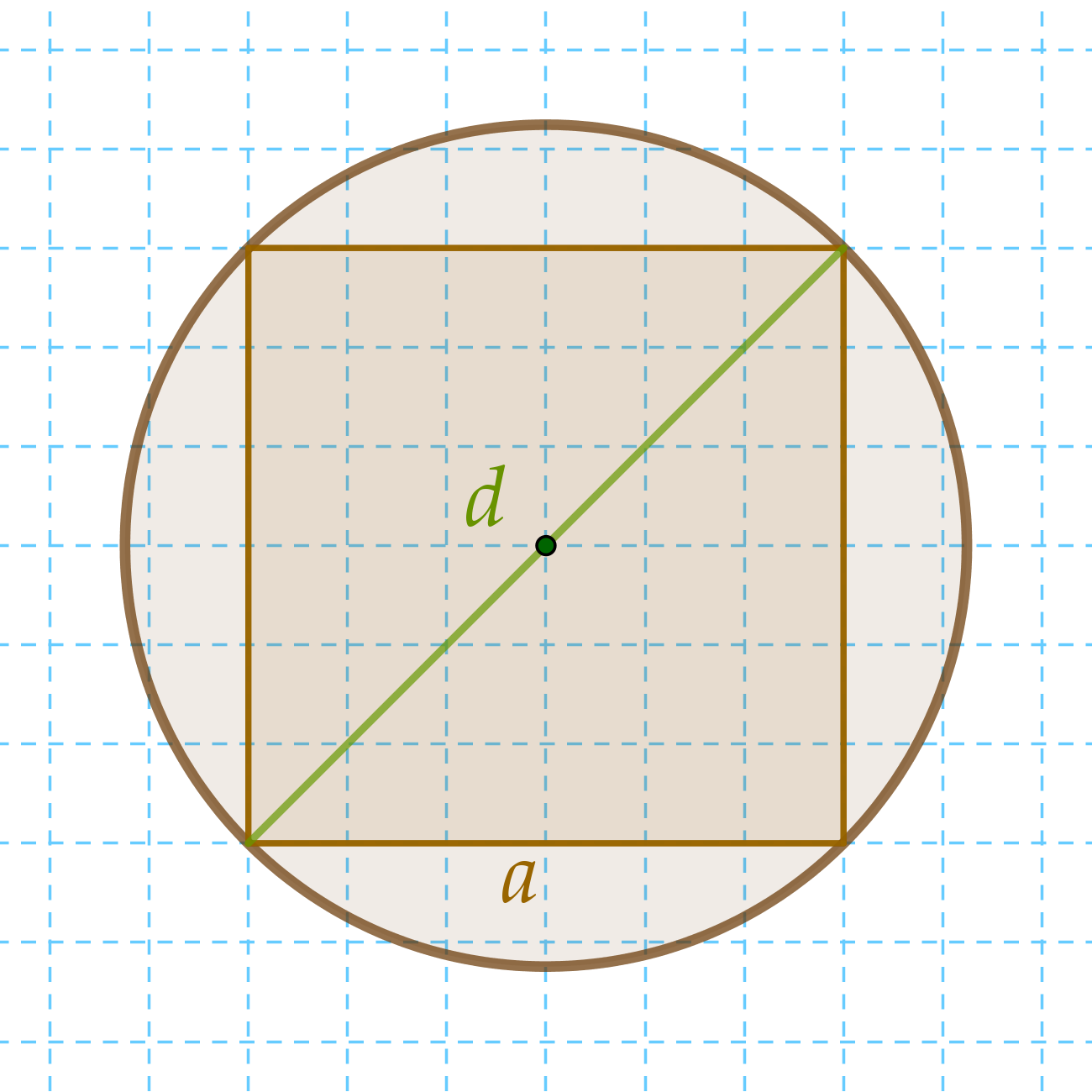
Ebből kell kiszámolni a négyzet oldalát, a-t. Ezt megtehetjük Pitagorasz-tétellel: a² + a² = d². Ebből az jön ki, hogy a = 0,424 m.

Most számoljuk ki a hasáb térfogatát. A hasáb térfogata: alapterület szorozva a hasáb magasságával: V = T_alap·m. Az alapterület a négyzet területe: T_alap = T_négyzet = a² = 0,424² = 0,18 m². A hasáb magassága pedig a gerenda hossza, ami m = 5 m. Ezért a hasáb térfogata: V = 0,18 m² · 5 m = 0,9 m³. Ez pedig kisebb 1 m³-nél, ezért az állítás igaz.

b) Először azt kell kiszámolni, hogy 1 m³ deszkaáru eladásához hány m³ faanyagot kell vásárolni. Mivel a fa 40%-a hulladék, ezért a 60%-ából lesz deszka. Azt kell kiszámolni, hogy hány m³-nek a 60%-a 1 m³? x-nek a 60%-a 1. Ez egyenletben felírva: $$ x \cdot 0,6 = 1 \qquad /:0,6 $$ $$ x = 1,667 $$

Mivel 1 m³ nyers fa ára 30 000 Ft, ezért 1,667 m³ ára 1,667 · 30 000 = 50 000 Ft.

1 m³ deszkát 90 000 Ft-ért eladnak, de ennek 35%-a költség: 90 000 · 0,35 = 31 500 Ft.

Eddig tehát van 50 000 Ft + 31 500 Ft = 81 500 Ft költsége és 90 000 Ft bevétele a cégnek. A haszon a bevétel és a költség különbsége: 90 000 Ft - 81 500 Ft = 8 500 Ft.

c) A valószínűséget úgy számoljuk, hogy kedvezőperösszes, azaz a kedvező esetek száma per az összes lehetőség száma.

Kezdjük az összes lehetőség számával: Azt kell kiszámolni, hogy hányféle sorrendben mehet 4 fenyőt és 2 tölgyfát szállító teherautó. Mivel számít a sorrend és minden teherautót sorba teszünk, ezért permutációval számolunk, mégpedig ismétléses permutációval, mert vannak ugyanolyan teherautók. Ezért az összes sorrend: $$ \frac{6!}{4!\cdot 2!}=\frac{720}{24\cdot 2}=\frac{720}{48}=\color{DarkMagenta}{15} $$

A kedvező esetekhez a 2 tölgyfát szállító teherautó egymás után megy, ezért vegyük egynek ezt a két teherautót. Így lesz 4 fenyőt és 1 tölgyet szállító autó. Ez 5 jármű, aminek az összes lehetséges sorrendje kell, amit megint ismétléses permutációval számítunk: $$ \frac{5!}{4!}=\frac{120}{24}=\color{ForestGreen}{5} $$

Most már kiszámíthatjuk a valószínűséget: $$ p=\frac{\color{ForestGreen}{\mathrm{kedvező}}} {\color{DarkMagenta}{\mathrm{összes}}} =\frac{\color{ForestGreen}{5}}{\color{DarkMagenta}{15}} =\frac{1}{3}=0,333 $$

Tehát a valószínűség \$\frac13$\.