Hogyan oldjunk meg matek érettségit?
Nézzük meg a 2008-as matek középszintű érettségi megoldását!
I. rész
1. Adja meg a\$ ]-\frac{3}{8}; -\frac{1}{8}[ $\ nyílt
intervallum két különböző elemét!
Mit jelent ez? Két olyan számot keresünk, ami \$ -\frac{3}{8} $\-nál
nagyobb és \$ -\frac{1}{8} $\-nál kisebb. Például a \$ -\frac{2}{8} $\ ilyen. De kéne még egyet
találni. Lehet, hogy így tört alakban nehéz átlátni, ezért írjuk át
tizedestört alakba: \$ -\frac{3}{8} $\ = -3 : 8 (-3-ban a 8)= -0,375 (Számológéppel!),
\$ -\frac{1}{8} $\= -1 : 8=-0,125. Így már látszik, hogy pl. a -0,2 is jó, ami \$ -\frac{1}{5} $\.
(Megint csak számológép!) Mellesleg a feladat nem írja, hogy milyen
alakban kéri a két elemet (tehát tört vagy tizedestört), ezért nem is
kell arra törekedni, hogy tört legyen. Jó lesz az tizedestörtben is.
2. Egy 7-tagú társaságban mindenki
mindenkivel egyszer kezet fogott. Hány kézfogás történt?
Ha másként nem megy a feladat, meg lehet úgy is oldani, hogy
rajzolunk 7 pöttyöt (ezek az emberek), és minden pöttyöt összekötünk
minden pöttyel (az összekötés jelenti a kézfogást). Összesen 21 vonal
lesz, tehát hamar meg lehet számolni, úgyis csak a beírt választ nézik,
nem azt, hogy hogyan számoltuk ki. De ha végiggondoljuk, akkor is ez jön
ki: Ha hét ember van, akkor mindenki 6 másik emberrel fog kezet. 7
ember szorozva 6 kézfogással = 42. Ezzel a számolással viszont
beleszámoltuk azt, amikor én kezet fogok Józsival, meg azt is, amikor
Józsi kezet fog velem, márpedig ez csak 1 kézfogás. Ezért a 42-t
osztani kell 2-vel, mert minden kézfogást kétszer számoltunk. Így kijön
a 21. Az érettségi írói is így gondolkoztak, mert 1 pontot adnak, ha a
válasz 42.
3. Péter egy 100-nál nem nagyobb pozitív
egész számra gondolt. Ezen kívül azt is megmondta Pálnak, hogy a gondolt szám 20-szal osztható.
Mekkora valószínűséggel találja ki Pál elsőre a gondolt számot, ha jól
tudja a matematikát?
Először a feladat első részével foglalkozzunk. Milyen
számokra gondolhatott Péter? A legkisebb pozitív egész, ami 20-szal
osztható, az maga a 20. Ezután 20-asával kell haladnunk: 40, 60, 80,
100. A 100 is jó, mert nem nagyobb, mint 100. Ez összesen 5 lehetőség.
Most jön a valószínűség. Ezt sem kell túlbonyolítani, csak azt kell
megjegyezni, hogy a valószínűséget mindig úgy számoljuk ki, hogy
kedvezőperösszes, azaz a kedvező esetek száma per az összes lehetőség
száma. Az összes lehetőségeket előbb írtuk fel, ez 5. Hiszen Pál tudja,
hogy Péter csak ezek közül választott. Mennyi a kedvező lehetőség? Ez
1, hiszen Péter 1 számra gondolt az 5 közül. Ezért a valószínűség:
\$ \frac 15 $\=20%.
4. Ha fél kilogramm narancs 75 Ft-ba
kerül, akkor hány kilogramm narancsot kapunk
300 Ft-ért?
Kezdjük úgy, hogy ha fél kg narancs 75 Ft, akkor 1 kg a
kétszeresébe kerül, ami 150 Ft. A 300 Ft meg éppen a 150 kétszerese,
ezért 2 kg narancsot vehetünk. Nem érdemes tovább bonyolítani.
5. Adja meg a valós számok halmazán
értelmezett x ↦ x2
- 5x másodfokú függvény zérushelyeit! Számítsa ki a függvény helyettesítési értékét az 1,2 helyen!
A zérushelyeket úgy kapjuk meg, hogy megoldjuk az x2 - 5x = 0 egyenletet. Ami egy másodfokú egyenlet, ezért megoldhatjuk a megoldóképlettel (benne van a függvénytáblázatban). De azért ennél van egyszerűbb megoldás is, csak észre kell venni, hogy ez hiányos másodfokú egyenlet. Emeljünk ki x-et: x · (x - 5) = 0. Ez egy szorzat, márpedig egy szorzat akkor nulla, ha valamelyik tagja nulla. Tehát vagy x = 0, vagy x - 5 = 0. Ezért a két megoldás 0 és 5.
És mi lehet a helyettesítési érték? Ezt meg úgy kapjuk meg,
hogy x helyére beírjuk az 1,2-t: 1,22
- 5 · 1,2 = 1,44 - 6 = -4,56.
6. Az ABCD négyzet
középpontja K, az AB oldal
felezőpontja F. Legyen a = KA
és
b = KB . Fejezze ki az a
és b vektorok segítségével a KF
vektort!
Hogy könnyebben lássuk, miről van szó, rajzoljunk! Egy
négyzetet kell rajzolni, ennek csúcsait jelölni A, B, C és D-vel.
A négyzet középpontját K-val, az AB
oldal felezőpontját F-fel jelöljük:
Rajzoljuk be a vektorokat is:
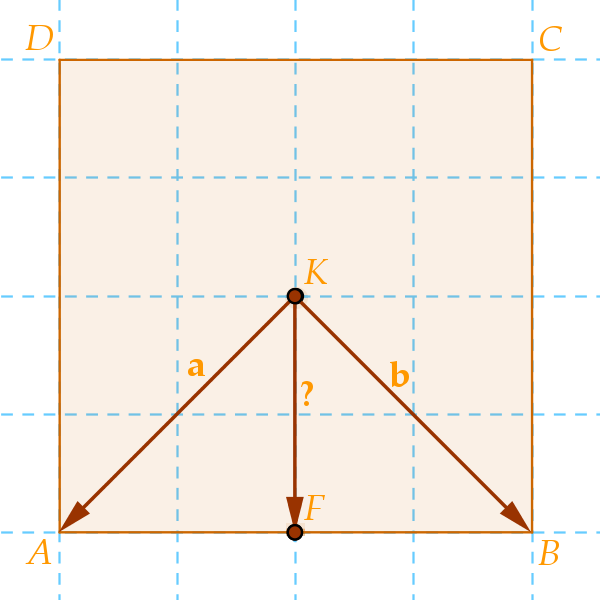
A kérdéses vektor az ábrán ?-lel van jelölve.
Így lerajzolva már jobban látjuk, mit is kérdez a feladat.
Igazából egy szakasz felezőpontjába mutató vektort kell megadni a
végpontokba mutató vektorok segítségével. Ebben az esetben az, hogy ez
egy négyzetben van, csak figyelemelterelés. A felezőpontba mutató
vektor a két végpontba mutató vektor átlaga: \$ \frac{\mathbf{a}+\mathbf{b}}{2} $\.
7. Adja meg az alábbi állítások
igazságértékét (igaz vagy hamis), majd döntse el, hogy a b) és a c)
jelű állítások közül melyik az a) jelű állítás megfordítása!
- a) Ha az ABCD négyszög téglalap, akkor átlói felezik egymást.
- b) Ha az ABCD négyszög átlói felezik egymást, akkor ez a négyszög téglalap.
- c) Ha az ABCD négyszög nem téglalap,
akkor átlói nem felezik egymást.
Hogyan tudjuk eldönteni az első állításról, hogy igaz-e? Ha
rajzolunk egy téglalapot, és berajzoljuk az átlóit, akkor meglátjuk,
hogy azok felezik-e egymást.
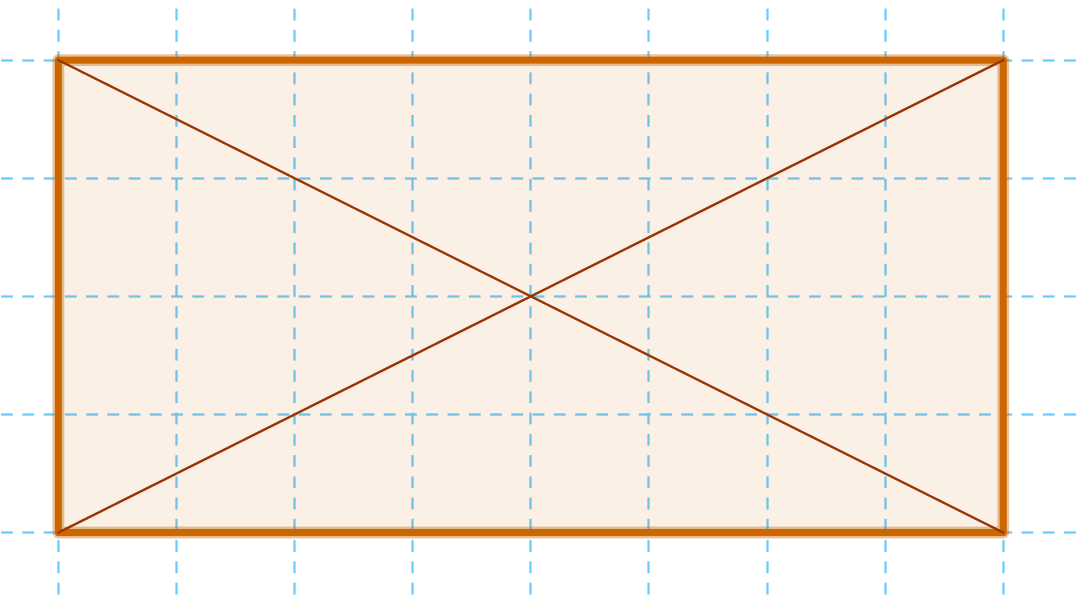
Ennek a téglalapnak felezik egymást. De vajon minden
téglalapnak? A válasz az, hogy igen, mert még a paralelogrammának is
felezi, és ugye minden téglalap paralelogramma. Tehát az a) állítás
igaz.
A második kérdésre úgy kaphatjuk meg a választ, hogy
rajzolunk két szakaszt, amik felezik egymást:
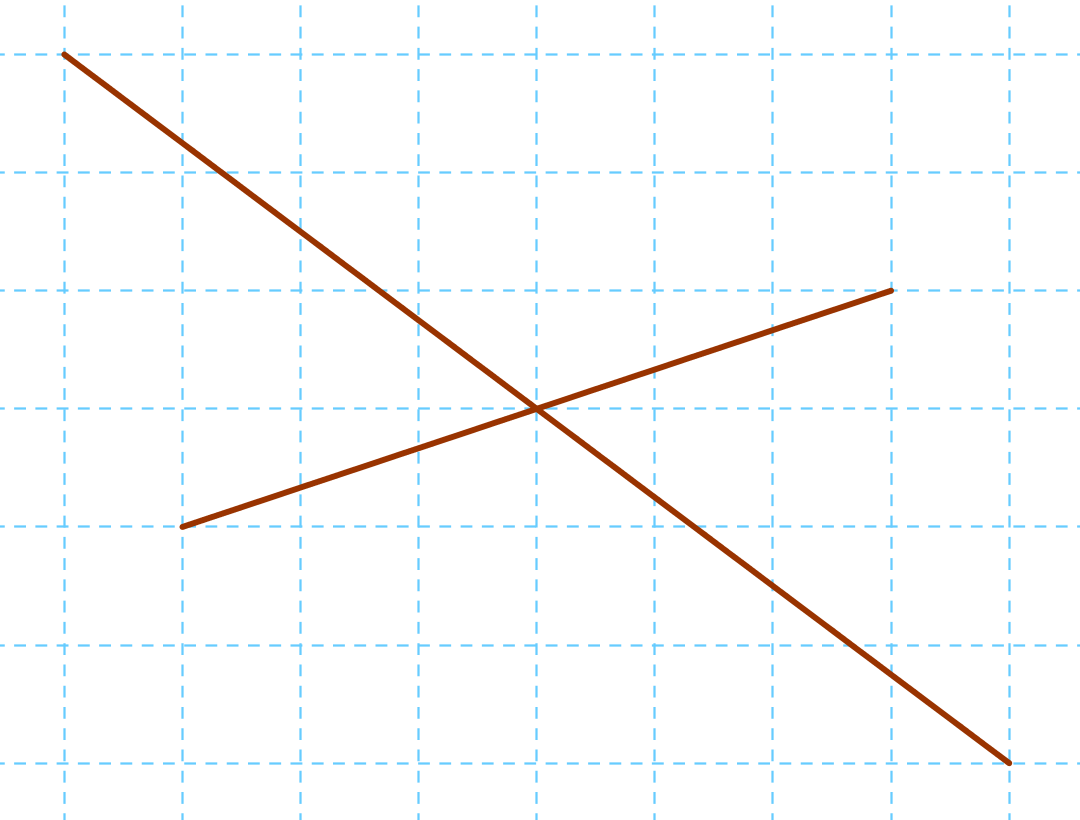
Ezek lesznek egy négyszög átlói. Most kössük össze a
szakaszok végpontjait:

Amit kaptunk, az láthatóan nem téglalap, hanem
paralelogramma. Tehát a b) kérdésre a válasz: hamis.
Végül a harmadik állítás: az eddigiek alapján tehát a
paralelogrammák átlói is felezik egymást, ezért ha egy négyszög nem
téglalap, hanem például paralelogramma, akkor az átlói felezhetik
egymást. Ezért a c) is hamis.
A feladat utolsó részéhez azt kell tudni, hogy mit jelent egy
állítás megfordítása. A feladat három állításában valamiből következett
másvalami. Azaz: Ha „valami”, akkor „másvalami”. Ennek megfordítását úgy
kapjuk meg, ha a következtetés irányát megfordítjuk: Ha „másvalami”,
akkor „valami”. Az a) állításban a valaminek a „téglalap” felel meg, a
másvalaminek pedig az „átlói felezik egymást”. Ha ezt a kettőt
felcseréljük, megkapjuk a b) állítást. Érdekes módon a c) állítás is
tekinthető az a) megfordításának, mert a c) logikailag ugyanaz, mint a
b). Ezért a c)-t is elfogadják helyes válasznak. (Akik ebben az évben
írták az érettségit, 1 potyapontot ezzel már szereztek is :-))
Még egy megjegyzés: csak azért, mert az a) igaz, a másik
kettő hamis, még nem lesznek automatikusan az a) megfordításai. Sőt:
vannak olyan igaz állítások, amiknek a megfordításuk is igaz. Ilyen
például a Pitagorász-tétel.
8. Írja fel két egész szám hányadosaként a
2+\$ \frac{2}{3} $\ szám reciprokának értékét!
Azt ugyebár tudjuk, hogy egy tört reciprokát úgy kapjuk meg,
hogy a felső és az alsó számot felcseréljük. Hát akkor ebből a
2+\$ \frac{2}{3} $\-ból kéne egy törtet csinálni. Végezzük el az összeadást. Törteket
úgy kell összeadni, hogy közös nevezőre hozunk. Mivel az első szám nem
tört, a második pedig igen, ezért a közös nevező a második tört
nevezője lesz: ez 3. A 2-ből hogy csinálunk törtet? Úgy is feltehetjük
a kérdést, hogy minek a harmada 2? Hát a 6-nak. Ezért 2 =\$ \frac{6}{3} $\. \$ \frac{6}{3} $\-ot
és \$ \frac{2}{3} $\-ot már simán össze tudunk adni: \$ \frac{6}{3} $\ + \$ \frac{2}{3} $\ = \$ \frac{8}{3} $\. És a \$ \frac{8}{3} $\-ot meg már
könnyen meg tudjuk fordítani: \$ \frac{3}{8} $\.
9. Mennyi az f(x)
= - |x| + 10 ( x ∈ \$ \mathbb{R} $\ ) függvény
legnagyobb értéke, és hol veszi fel ezt az értéket?
Ha semmi fogalmunk nincs a függvényekről, akkor készítsünk
táblázatot, amiben vízszintesen az x értékek vannak
(x ugye felveszi az összes lehetséges értéket, azaz
az összes valós számot, de erre az érettségi ideje kevés), függőlegesen
pedig az f(x) értékek, amiket
úgy számolunk ki, hogy a képletben x helyére
beírunk egy számot. Például: ha x = -3, akkor f(x)
= - |-3| + 10 = -3 + 10 = 7. Így kapjuk meg az alábbi táblázatot:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| f(x) | 7 | 8 | 9 | 10 | 9 | 8 | 7 |
Ábrázoljuk a táblázat adatait koordináta-rendszerben:
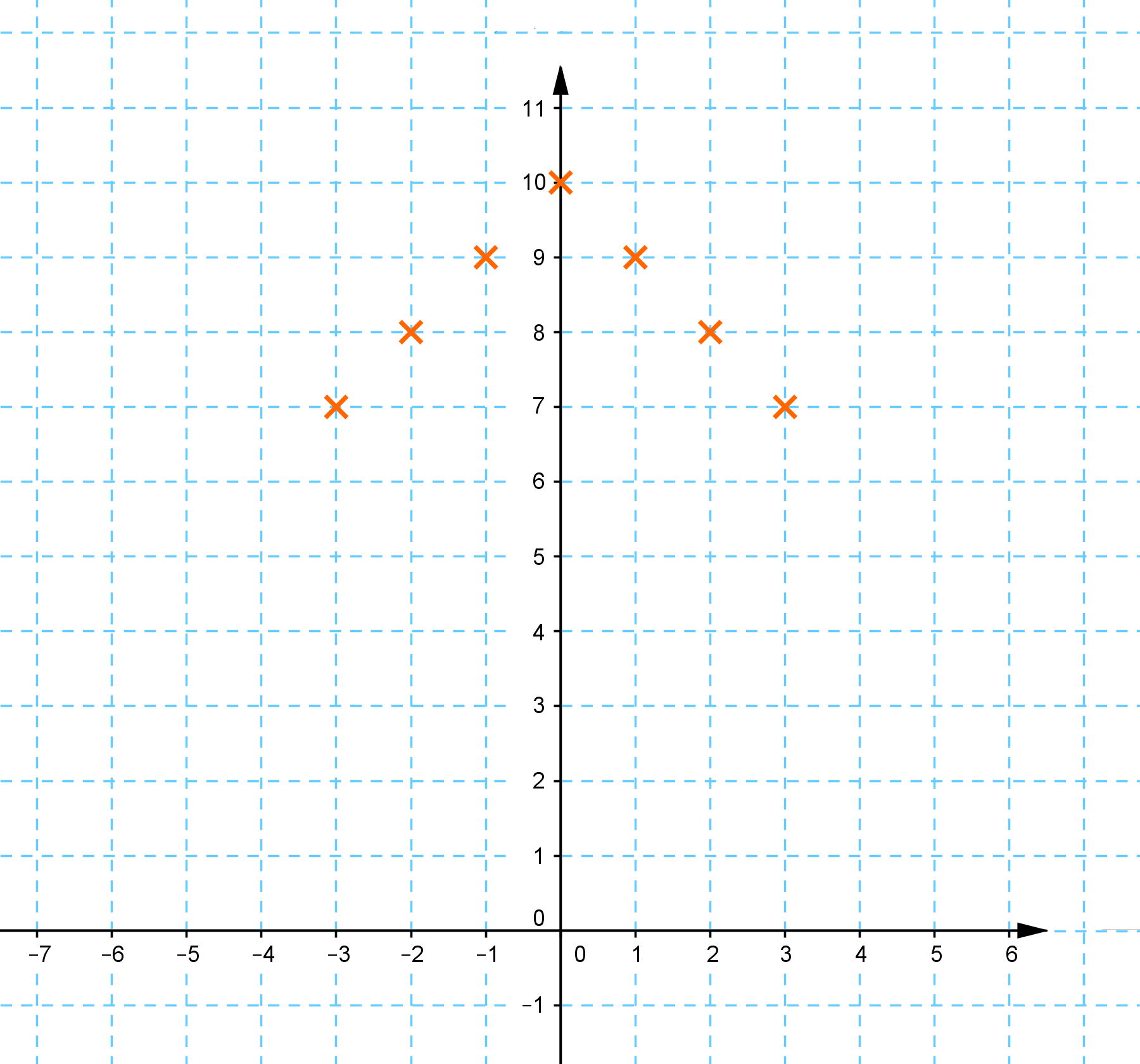
Így látható, hogy a függvény legnagyobb értéke 10 (ezt az y
tengelyen veszi fel), és ezt az x = 0 helyen veszi
fel.
10. Egy számtani sorozat első tagja –3,
differenciája –17. Számítsa ki a sorozat
100-adik tagját! Számítását részletezze!
Az érettségi első részébe általában olyan sorozatos példákat
tesznek, amiket képletek nélkül is ki lehet számolni. Na ez nem ilyen.
Tehát a függvénytáblázatból ki kell keresni a sorozat n-dik
tagját megadó képletet: an =
a1 + (n -
1)d.
A feladatot kezdjük azzal, hogy megnézzük, mi van megadva. Az
első tag: a1 = -3, a
differencia: d = -17 és n = 100.
Ezeket kell behelyettesíteni a képletbe: a100
= -3 + (100 - 1) · (-17) = -3 + 99 · (-17) = -3 + (-1683) = -1686.
Ezzel kész is a feladat.
11. Egyszerűsítse az \$ \frac{x+8}{x^2+8x} $\ algebrai törtet! Tudjuk, hogy x
∈ {-8 ; 0}.
Nagyon gyanús, hogy a számlálóban és a nevezőben is van 8-as, de ez nem jelenti azt, hogy 8-cal lehet egyszerűsíteni. Inkább a nevezőben emeljünk ki x-et: \$ \frac{x+8}{x(x+8)} $\ . Így most a zárójelben ugyanaz van, mint fölül, és mivel a nevezőben szorzat van, x + 8-cal egyszerűsíthetünk \$\require{cancel} \frac{\cancel{x+8}}{x(\cancel{x+8})} = \frac{1}{x} $\
12. Egy fordítóiroda angol és német
fordítást vállal. Az irodában 50 fordító dolgozik,
akiknek 70%-a angol nyelven, 50%-a német nyelven fordít.
Hány fordító dolgozik mindkét nyelven? Válaszát indokolja!
Az ilyen típusú feladat megoldásában nagyon sokat segít egy
halmazábra. Rajzoljunk két kört, az egyikbe az angolul fordítók, a
másikba a németül fordítók kerülnek. A közös részbe (a halmazok
metszetébe) a mindkét nyelven fordítók kerülnek.
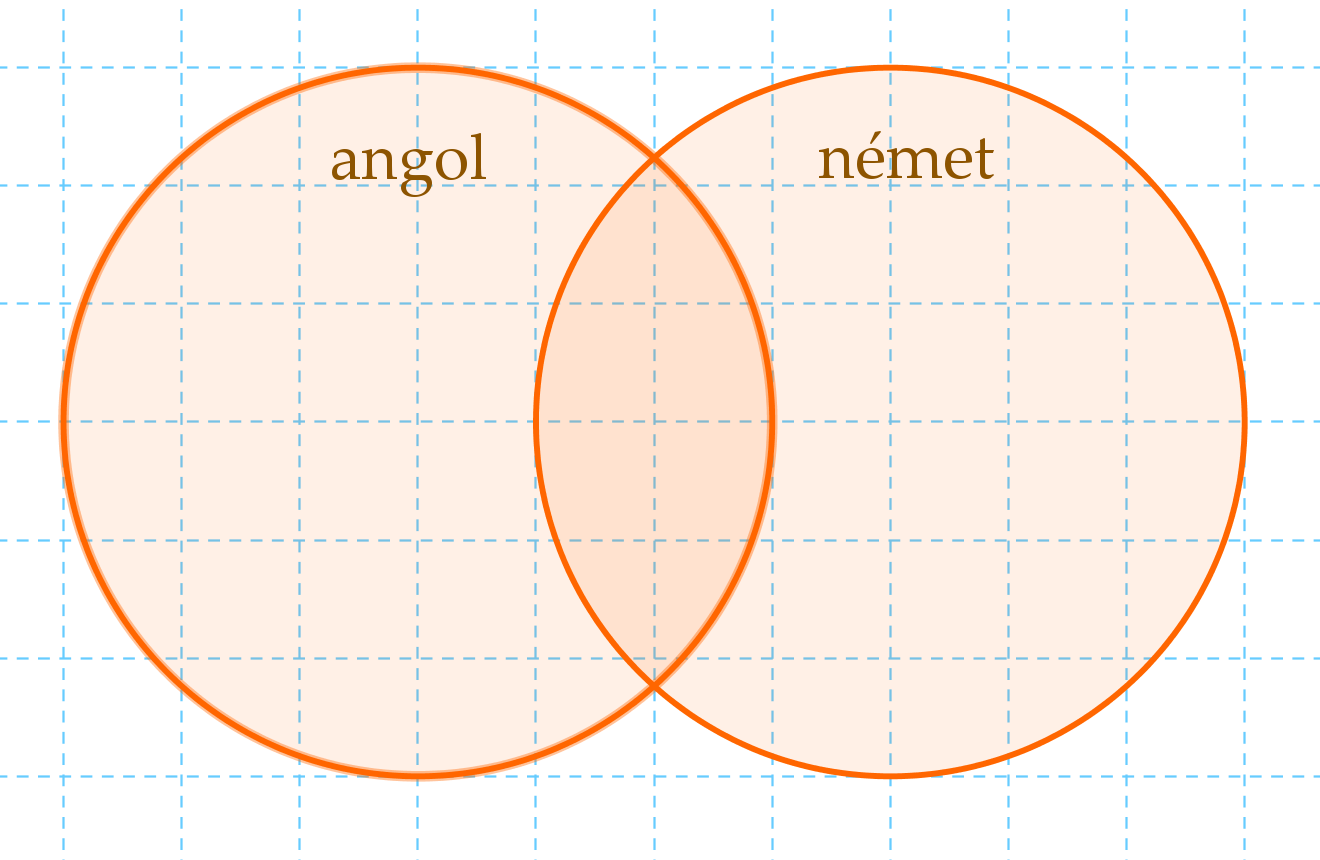
Tudjuk, hogy összesen 50 fordító van, ezek 70%-a angolul
fordít, ezért 50-nek a 70%-át kell kiszámolni: 50 · 70 :100 = 35.
Ugyanígy a német fordítók: 50 · 50 :100 = 25. A mindkét nyelven
fordítókat nem tudjuk, ismeretlen, ezért jelöljük x-szel.
A 35 angolul fordító közül x németül is fordít, a
maradék pedig csak angolul. A maradék 35 - x.
Ugyanígy a csak németül fordítók száma: 25 - x. A
halmazábra középső részébe kerül x. A bal oldali
részben a csak angolul fordítók vannak, ide ezért 35 - x
kerül, a jobb oldali részbe pedig 25 - x.
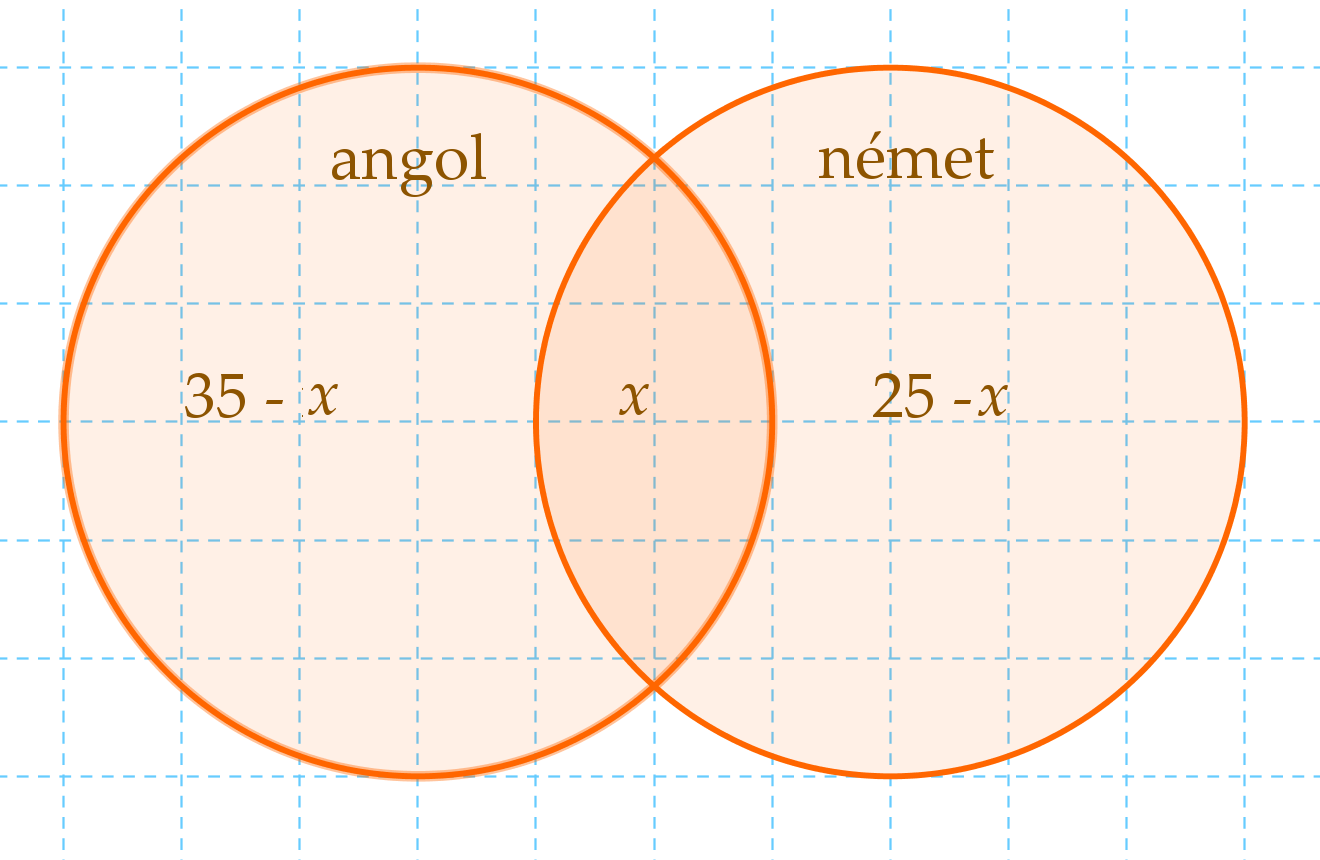
Ha összeadjuk a 3 halmazrészbe kerülő számokat, annak ki kell
adnia az összes fordítót, azaz 50-et:
35 - x + x + 25 - x
= 50
Ezt az egyenletet kell megoldani x-re. A
megoldás: x = 10.
II. rész
A
13. Oldja meg a valós számok halmazán a
következő egyenleteket!
a) \$ \lg(x+15)^2-\lg(3x+5) = \lg 20 $\
b) \$ 25^\sqrt{x}=5\cdot 5^{3\sqrt{x}} $\
Elsőre elég nehéznek tűnhet ez a két egyenlet, de nem olyan
bonyolult. Persze, aki először találkozik logaritmussal, annak az.
Nyissuk ki a függvénytáblázatot a logaritmusnál, és ott lesz egy ilyen
képlet:
$$
\log_{a}\left(\frac xy \right) = \log_a x-\log_a y
$$
Ez egy egyenlőség, ami oda-vissza igaz, tehát akár fordítva
is írhattuk volna:
$$
\log_a x-\log_a y = \log_{a}\left(\frac xy \right)
$$
Ráadásul itt most 10-es alapú logaritmus van, ezt jelenti az
lg, ezért a képletet így is átírhatjuk:
$$
\lg x-\lg y = \lg\left(\frac xy \right)
$$
A feladat egyenletének bal oldalán ugyanígy két logaritmus
(azaz lg) van kivonva egymásból, csak x és y
helyett valamilyen zárójeles dolgok vannak. Vegyük úgy, hogy az első
zárójeles dolog a négyzetreemeléssel együtt x, a
másik zárójeles dolog pedig y:
$$
\lg \underbrace{(x+15)^2}_x-\lg \underbrace{(3x+5)}_y = \lg 20
$$
Most erre alkalmazzuk a függvénytáblázat képletét.
$$
\lg \left(\frac{(x+15)^2}{3x+5}\right) = \lg 20
$$
A következő lépéshez azt kéne észrevenni, hogy az egyenlet
mindkét oldalán egyetlen lg van. Ezért idézőjelben „elhagyható” az lg,
olyan mintha egyszerűsítenénk vele. Valójában jobban járunk, ha a
következő mondatok valamelyikét írjuk oda:
- Mivel a logaritmus függvény kölcsönösen egyértelmű ...
- Mivel a logaritmus függvény szigorúan monoton ...
Ha elhagyjuk az lg-t, ez marad:
$$
\frac{(x+15)^2}{3x+5} = 20
$$
Ez már egy sima, bár törtes egyenlet. Szorozzunk át a
nevezővel:
$$
(x+15)^2 = 20\cdot (3x+5)
$$
A bal oldalon emeljünk négyzetre, és figyeljünk arra, hogy (a
+ b)2 = a2
+ 2ab + b2.
A jobb oldalon is bontsuk fel a zárójelet.
$$
x^2 + 30x + 225 = 60x +100
$$
Ez egy másodfokú egyenlet, tehát akkor járunk el a legjobban,
ha 0-ra rendezzük. Ami azt jelenti, hogy a jobb oldalról mindent
eltüntetünk, azaz kivonunk 60x-et és 100-at:
$$
x^2 - 30x + 125 = 0
$$
Másodfokú egyenletet megoldóképlettel oldunk meg. Csakazértsem
fogom leírni a mínuszbépluszmínuszgyökalatt... másodfokú
megoldóképletet, ki kell keresni a függvénytáblázatból (de sokkal jobb
lenne fejből tudni, legalább ezt). Megoldásnak azt kapjuk, hogy x1
= 5 és x2 = 25
Hogy jó eredmény jött-e ki, azt visszahelyettesítéssel
ellenőrizhetjük. És ha már itt tartunk, mivel logaritmusos egyenlet
volt, nem ártott volna kikötni az elején. (Ha csak a feladat végén jut
eszünkbe, az nem gond, utólag visszaírhatjuk az elejére. :-)) De miért
is kell kikötni? Mert a logaritmus függvény csak 0-nál nagyobb számokra
van értelmezve. Ezért az lg utáni zárójeles részeknek 0-nál
nagyobbaknak kell lenniük. Az első esetben valaminek a négyzete van.
Márpedig minden szám négyzete pozitív, kivéve a 0-át, mert annak 0 a
négyzete. Ezért x nem lehet egyenlő -15: x
≠ -15. A második esetben 3x - 5-nek kell 0-nál
nagyobbnak lennie: 3x - 5 > 0. Ennek
megoldása x > -\$ \frac 53 $\. Mivel -15 < -\$ \frac 53 $\,
ezért a -15-tel nem kell foglalkozni. A megoldásban kijött 5 és 25
nagyobbak -\$ \frac 53 $\-nál, ezért jó megoldások.
b) \$ 25^\sqrt{x}=5\cdot 5^{3\sqrt{x}} $\
A logaritmusnál rájöttünk, hogy kikötéssel kell kezdeni,
kezdjük hát ezt a feladatot a kikötéssel. Gyöknél azt kell kikötni,
hogy negatív szám nem lehet gyök alatt, ezért x ≥
0. Ennyi a kikötés.
Az egyenlet megoldásához most sincs más dolgod, mint kinyitni
a függvénytáblázatot a hatványozás azonosságainál. Ott van egy ilyen
egyenlet:
$$
(a^n)^m = a^{n\cdot m}
$$
Miért is kell ez nekünk? Mert a feladat bal oldalán lévő
25-öt átírhatjuk 52-re. Ezért az azonosságban a-t
írjuk át 5-re, az n-et 2-re, az m
pedig a \$ \sqrt{x} $\ legyen. Így ezt kapjuk:
$$
(5^2)^\sqrt{x} = 5^{2\cdot \sqrt{x}}
$$
Most az egyenlet jobb oldalához is keressünk egy azonosságot:
$$
a^n\cdot a^m = a^{n + m}
$$
Ebben is a legyen 5. Mivel 5 = 51,
ezért n legyen 1 és m legyen \$3\sqrt{x}$\:
$$
5^1\cdot 5^{3\sqrt{x}} = 5^{1 + 3\sqrt{x}}
$$
Most tegyük össze ezt a két eredményt, és írjuk be a feladat
egyenletébe:
$$
5^{2\cdot\sqrt{x}} = 5^{1 + 3\sqrt{x}}
$$
Ez már nekünk nagyon jó, mert mindkét oldalon egy darab 5-ös
van. Ezért a logaritmusnál megbeszélt mondatok miatt az 5-ösöket
elhagyhatjuk, és maradnak a kitevők:
$$
2\cdot\sqrt{x} = 1 + 3\sqrt{x}
$$
$$2\sqrt{x}$$-et kivonok mindkét oldalból:
$$
0 = 1 + \sqrt{x}
$$
És még 1-et is kivonok:
$$
-1 =\sqrt{x}
$$
Próbáljuk meg értelmezni ezt az eredményt: valaminek a gyöke
-1. A négyzetgyökvonásnak definíció szerint csak nemnegatív szám lehet
a végeredménye. Tehát ennek az egyenletnek nincs megoldása. Kész a
feladat.
Térjünk még vissza az utolsó egyenletre: mi van, ha valaki
négyzetre emel, mert el akarja tüntetni a gyökjelet? Azt kapja, hogy x
= 1. De ez nem jó megoldás, mert visszaellenőrizve \$ \sqrt{1} $\ = 1-et kapunk,
és nem \$ \sqrt{1} $\ = -1. Szóval egy egyenlet négyzetre emelése rossz
megoldáshoz is vezethet, ezért kell gyökös egyenleteknél mindig
ellenőrizni.
14. Adott a koordináta-rendszerben az A(9
; -8) középpontú, 10 egység sugarú kör.
a) Számítsa ki az y =
-16 egyenletű egyenes és a kör közös pontjainak koordinátáit!
b) Írja fel a kör P(1;-2)
pontjában húzható érintőjének egyenletét!
Adja meg ennek az érintőnek az iránytangensét (meredekségét)!
Ha egy feladatban alakzatok (kör, egyenes, stb.) egyenletéről
van szó, akkor az a feladat a koordináta-geometriából
van. Tehát érdemes a függvénytáblázatot annál a résznél kinyitni. (Van
olyan függvénytáblázat, ahol ez a témakör analitikus geometria
néven fut, de ez csak egy fellengzősebb elnevezése ugyanannak a
dolognak.) Keressük meg a kör egyenletét. Ott van egy ilyen ábra:
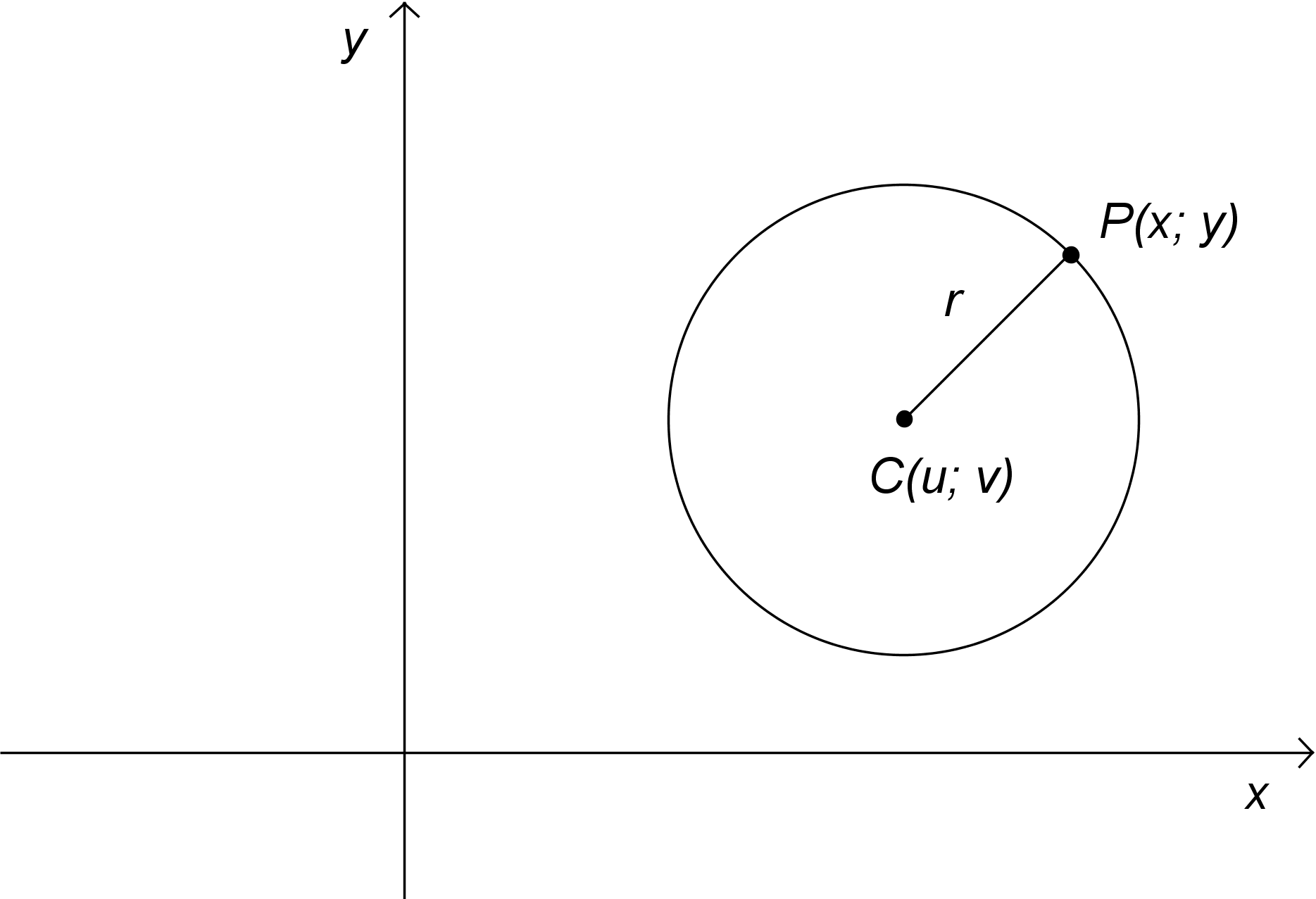
És alatta a kör egyenlete:
Itt a kör középpontja C-vel van jelölve,
a feladatban pedig A-val, a középpont koordinátái
pedig u-val és v-vel, a
feladatban pedig konkrétan meg van adva: 9 és -8. És még a sugár (r)
is adott: r = 10. A köregyenletben
behelyettesíthetjük u, v és r
értékét, x és y pedig marad x
és y:
Kicsit átalakítva:
És ha le is rajzoljuk, ezt kapjuk:

A következő, ami meg van adva a feladatban, az egy egyenes
egyenlet. Ha nem tudod lerajzolni, attól még megoldható a feladat, a
rajz csak megkönnyítheti a dolgot. Szóval próbáljuk meg értelmezni az y
= -16 egyenletet. A koordináta-rendszerben y minden
esetben -16-os értéket vesz fel, az x értékektől
függetlenül. Ez azt jelenti, hogy az egyenes az x-tengellyel
párhuzamos, és az y-tengelyt -16-nál metszi. Így
néz ki:
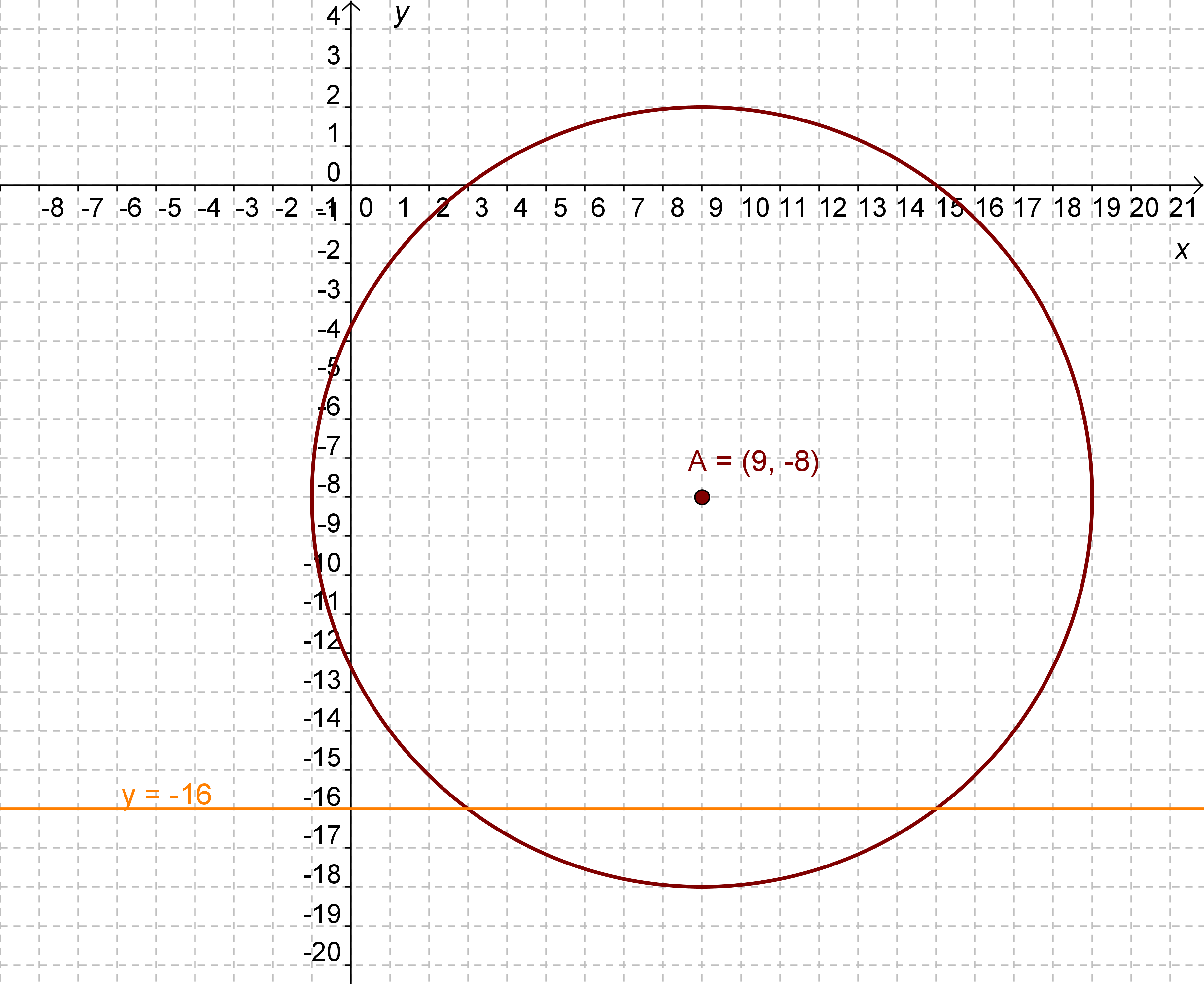
A feladatban a kör és az egyenes metszéspontjait kell
kiszámolni. Ez akár le is olvasható az ábráról, de az érettségin nem
hiszem, hogy bárki olyan pontos ábrát tudna rajzolni, hogy leolvashassa
(erre nem is kapna pontot). Az ábra arra viszont jó, hogy kb. látni
lehet, hogy hol vannak a metszéspontok. Jelöljük ezeket M1-gyel
és M2-vel.
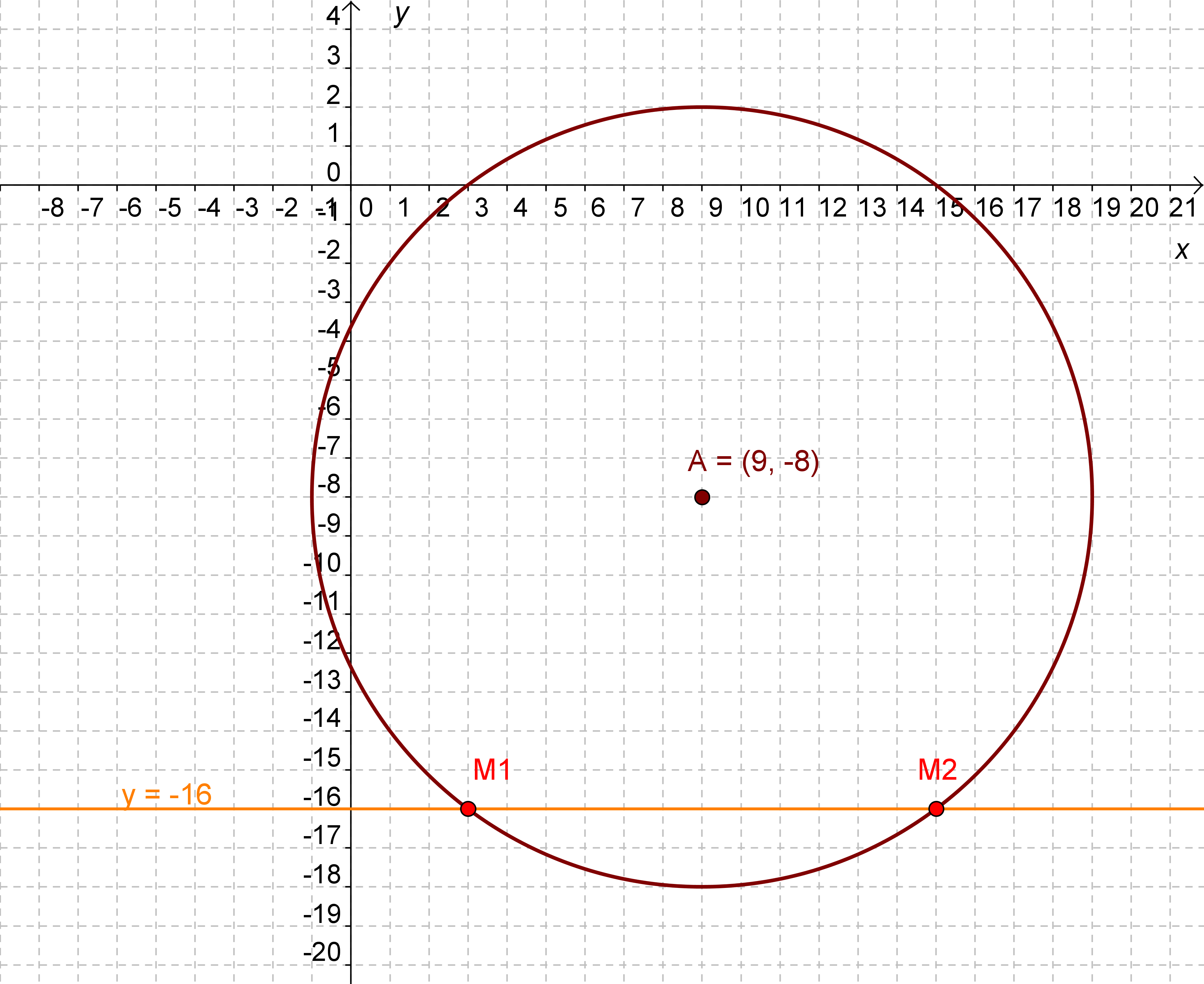
És most jön az, hogy hogy tudjuk kiszámolni. A
koordináta-geometriában azért van egyenlete az alakzatoknak, hogy a
metszéspontjaikat egyenletrendszerrel oldhassuk meg. Tehát adva van két
egyenlet:
(x - 9)2 + (y
+ 8)2 = 100
y = -16
És van két ismeretlenünk: x és y.
Sőt, az y már nem is ismeretlen, mert a második
egyenlet szerint -16 az értéke. Ezért az első egyenletben y
helyére máris beírhatunk -16-ot:
(x - 9)2 + (-16 + 8)2
= 100
(x - 9)2 + (-8)2
= 100
(x - 9)2 + 64 = 100
/-64
(x - 9)2 = 36 /√
x - 9 = ±6
Itt az utolsó egyenletben a gyökvonás miatt bejött egy ±.
Tehát két megoldás van:
x1 - 9 = 6 /+9
x1 = 15
és
x2 - 9 = -6 /+9
x2 = 3
Tehát az M1 és M2
pontoknak ezek lesznek az x koordinátáik, az y
pedig továbbra is -16:
M1=(3; -16) és M2=(15;
-16)
Az ábráról leolvashatjuk, hogy tényleg ezek a koordináták.
Most jön a feladat második része. Itt adva van egy pont, P(1;-2),
ami rajta van a körön. Ebbe a pontba kell érintőt rajzolni.
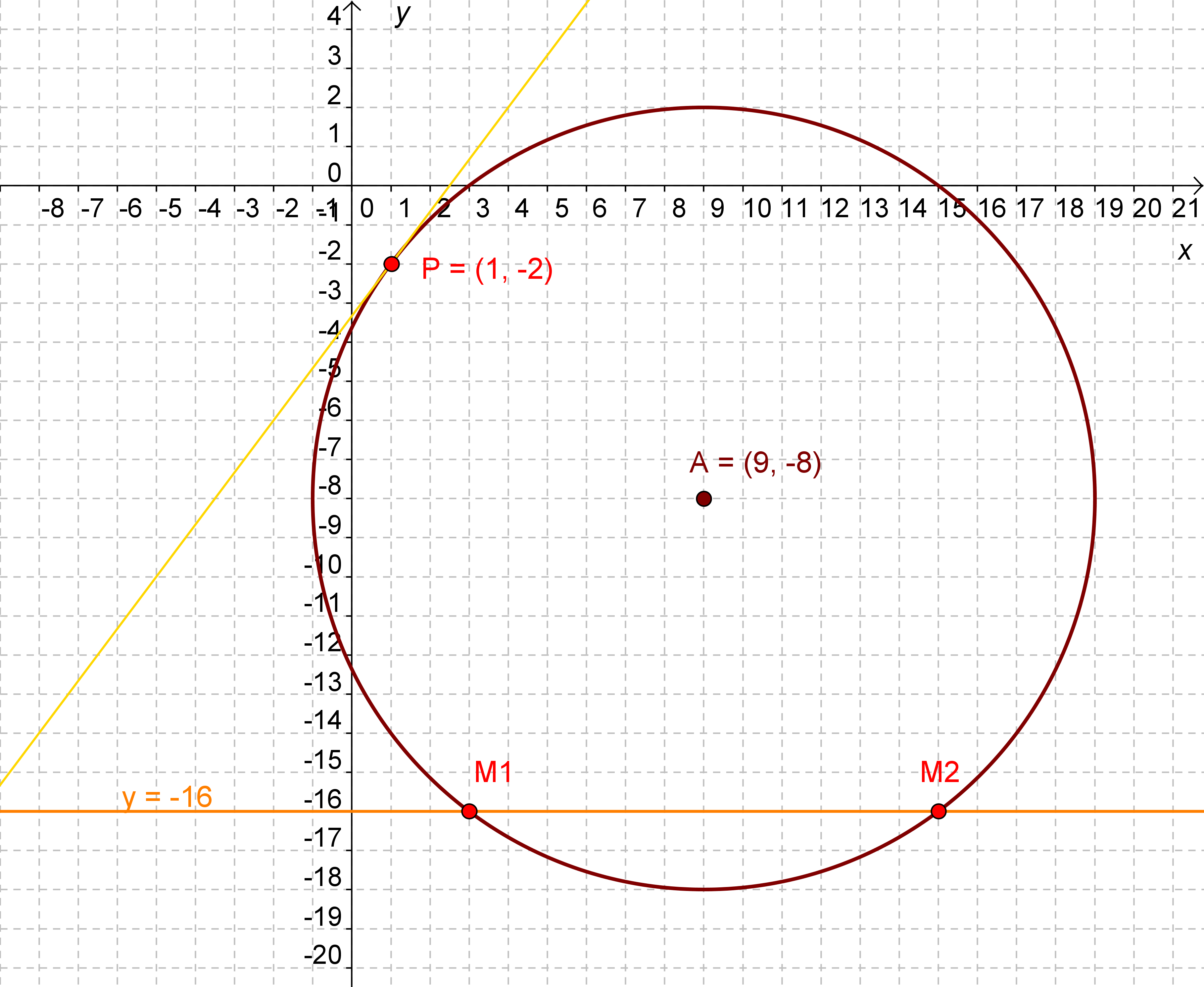
Az érintő egy egyenes, tehát egy egyenes egyenletet kell
felírni. Egy egyenesnek van irányvektoros, normálvektoros, stb.
egyenlete. Kérdés, hogy itt melyiket tudjuk használni. Az biztos, hogy
van egy pont, amin átmegy. De mit tudunk még? Vagy még egy pontot kéne
ismerni, vagy egy vektort. Azt kell tudni, hogy az érintési pontba
(ebben a feladatban a P pontba) húzott sugár
merőleges az érintőre. Tehát a sugárnak megfelelő vektor egy
normálvektor. Legyen ez a vektor az AP vektor, amit
n-nel jelöltem:
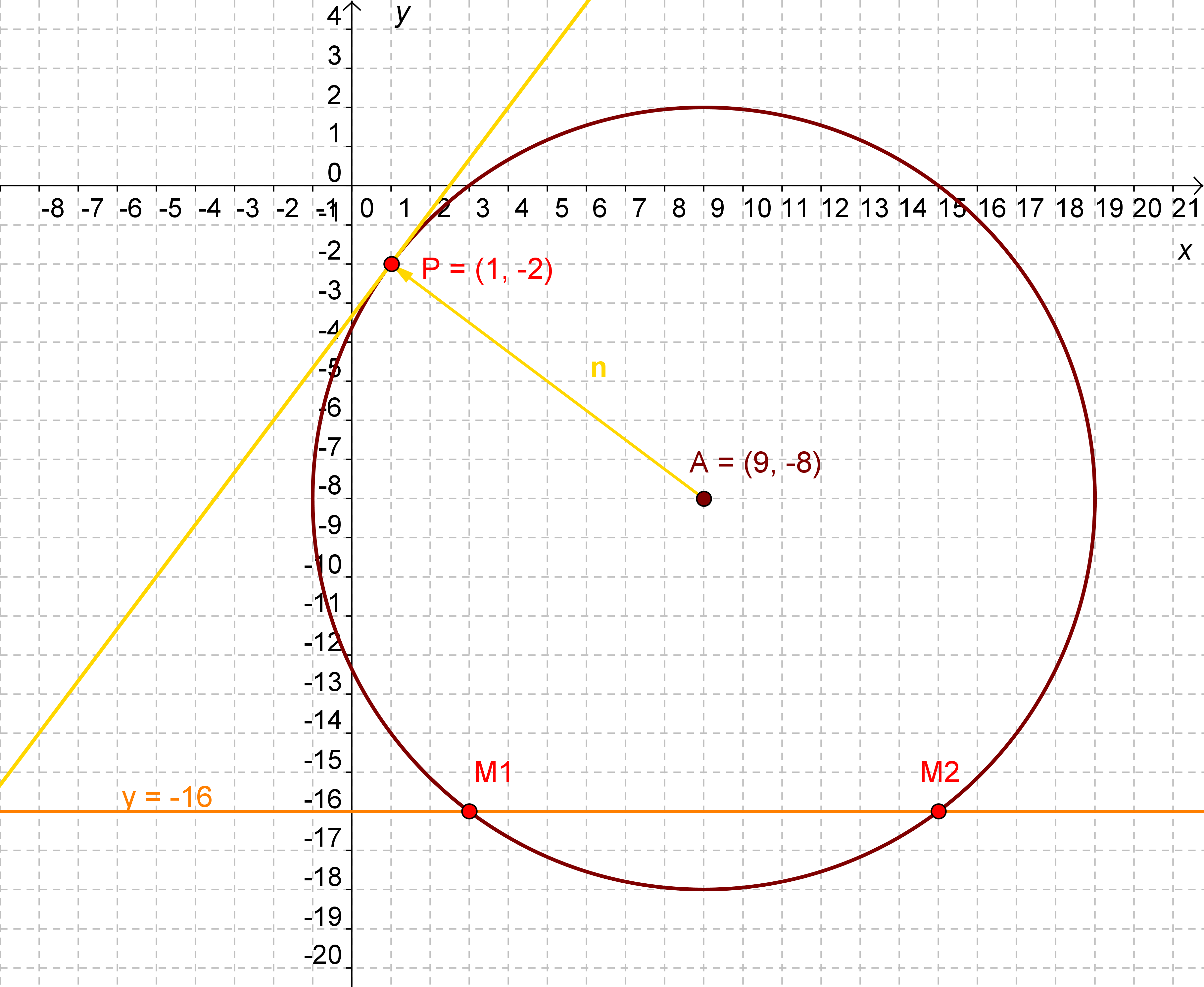
Egy vektor koordinátáit úgy határozzuk meg két pont
segítségével, hogy a pontok koordinátáit kivonjuk egymásból:
P(1;-2)
A(9 ; -8)
n = AP = (1-9;
-2-(-8)) = (-8; 6)
Az egyenes normálvektoros egyenlete a függvénytáblázat szerint:
Ax + By = Ax0 + By0
A és B a normálvektor koordinátái, x0 és y0 pedig az adott pont (azaz a P pont) koordinátái. Ezekkel felírhatjuk az egyenes egyenletét:
-8x + 6y = -8 · 1 + 6 ·
(-2)
-8x + 6y = -20 /:2
-4x + 3y = -10
Megvan az érintő egyenlete, most már csak a meredekséget kéne
meghatározni. Ehhez az egyenletből fejezzük ki y-t:
3y = 4x -10 /:3
y = \$\frac{4}{3} $\x -\$\frac{10}{3}$\
Ha az egyenes egyenlete ilyen formában van felírva, akkor a
meredekség az x előtti szám, azaz \$\frac{4}{3} $\.
15. Az 1, 2, 3, 4, 5, 6 számjegyek
felhasználásával ötjegyű számokat készítünk az összes
lehetséges módon (egy számjegyet többször is felhasználhatunk). Ezek
között hány
olyan szám van,
a) amely öt azonos számjegyből áll;
b) amelyik páros;
c) amelyik 4-gyel osztható?
Az a) feladat roppant egyszerű. Ha egy szám 5 azonos
számjegyből áll, akkor az vagy 5 darab 1-es, vagy 5 darab 2-es, vagy...
Mivel hatféle számjegy van, ezért hatféle ilyen ötjegyű szám van. Erre
a feladatra akkor is megkapjuk a 3 pontot, ha csak felsoroljuk ezt a
hat számot.
A b) feladatnál lehet úgy gondolkodni, hogy az összes szám fele páros, fele páratlan, mert a számjegyek fele is páros (2, 4, 6) és fele páratlan (1, 3, 5). Most már csak azt kéne tudni, hogy összesen hány ötjegyű számot tudunk gyártani. Az ilyen "hányféleképpen" típusú feladatokat úgy lehet könnyen megoldani, hogy pl. négyzeteket rajzolunk, amik a számjegyek helyiértékét jelentik. Mivel ötjegyű számokat kell csinálni, ezért 5 négyzetet rajzolok fel. Az első négyzet a tízezreseket, a második az ezreseket, ..., az ötödik pedig az egyeseket jelentik.
□ |
□ |
□ |
□ |
□ |
Ezután a négyzetek alá odaírjuk, hogy hány számjegy közül választhatunk. Első helyre 6 számjegy kerülhet, ezért 6-ot írunk alá:
□ |
□ |
□ |
□ |
□ |
||||
| 6 |
Mivel minden számjegyet többször is felhasználhatunk, ezért a
második helyre is 6 szám kerülhet:
□ |
□ |
□ |
□ |
□ |
||||
| 6 | 6 |
És így tovább, minden négyzet alá 6-os kerül, mert a
számjegyek nem fogynak el.
□ |
□ |
□ |
□ |
□ |
||||
| 6 | 6 | 6 | 6 | 6 |
A négyzetek alá került számokat össze kell szorozni:
□ |
□ |
□ |
□ |
□ |
||||||||
| 6 | · | 6 | · | 6 | · | 6 | · | 6 | = | 65 | = | 7776 |
Tehát 7776 az összes lehetőség. Mivel megbeszéltük, hogy ennek
a fele páros, fele páratlan, ezért a megoldás: 7776:2 = 3888
Ezt az eredményt kapjuk akkor is, ha a négyzetes módszernél
az utolsó négyzet alá nem 6-ot írunk, hanem 3-at, mert csak akkor lesz páros az ötjegyű szám, ha az utolsó helyre 2, 4 vagy 6 kerül, ami három lehetőség:
□ |
□ |
□ |
□ |
□ |
||||||||
| 6 | · | 6 | · | 6 | · | 6 | · | 3 | = | 64 · 3 | = | 3888 |
A c) részhez néggyel oszthatónak kell lennie a számoknak.
Ehhez tudni kell a néggyel oszthatóság szabályát: az utolsó két
számjegyet kell nézni, és ha az osztható néggyel, akkor az egész szám
is osztható néggyel. Mire végződhet ezek szerint a szám? Fel kell
sorolni a néggyel osztható kétjegyű számokat (persze csak azokat,
amiben az 1, 2, 3, 4, 5, 6 szerepel):
12, 16, 24, 32, 36, 44, 52, 56, 64
Most nem magyarázkodok, hogy ez hogy jött ki, a szorzótáblát
kell tudni, ha meg nem, ott van a számológép.
Ez ugyebár 9 lehetőség az utolsó két helyre. Ha a négyzetekkel
akarunk számolni, akkor az utolsó két négyzetet vonjuk össze:
□ |
□ |
□ |
□□ |
Mivel az utolsó két számjegy 9-féleképpen alakulhat, ezért az
utolsó két négyzet alá 9-et írunk, az első 3 négyzet alá pedig továbbra
is hatot:
□ |
□ |
□ |
□□ |
|||||||
| 6 | · | 6 | · | 6 | · | 9 | = | 63 · 9 | = | 1944 |
Ezzel kész a feladat. Hozzátenném még, hogy az 1944 éppen a
7776-nak a negyede. Akkor miért nem lett volna elég azt írni, hogy
minden negyedik szám néggyel osztható, ezért az összes lehetőségnek
veszem a negyedét? Mert ez nem működik minden esetben, és azt is meg
kéne magyarázni, hogy itt miért működik.
B
16. Egy facölöp egyik végét csonka kúp
alakúra, másik végét forgáskúp alakúra formálták.
(Így egy forgástestet kaptunk.) A középső, forgáshenger alakú rész
hossza 60 cm és átmérője 12 cm. A csonka kúp alakú rész magassága 4 cm, a csonka kúp fedőlapja pedig 8 cm átmérőjű. Az elkészült cölöp teljes hossza 80 cm.
a) Hány m3 fára volt
szükség 5000 darab cölöp gyártásához, ha a gyártáskor a
felhasznált alapanyag 18%-a a hulladék? (Válaszát egész m3-re
kerekítve adja meg!)
Az elkészült cölöpök felületét vékony lakkréteggel vonják be.
b) Hány m2 felületet
kell belakkozni, ha 5000 cölöpöt gyártottak? (Válaszát egész m2-re
kerekítve adja meg!)
Ehhez a feladathoz nem kell térlátás, csak 3 testet kell
összerakni: felül csonkakúp, középen henger, alul kúp. Egy cölöp tehát
így néz ki:

Ha a feladatban megadott méreteket is berajzolom:
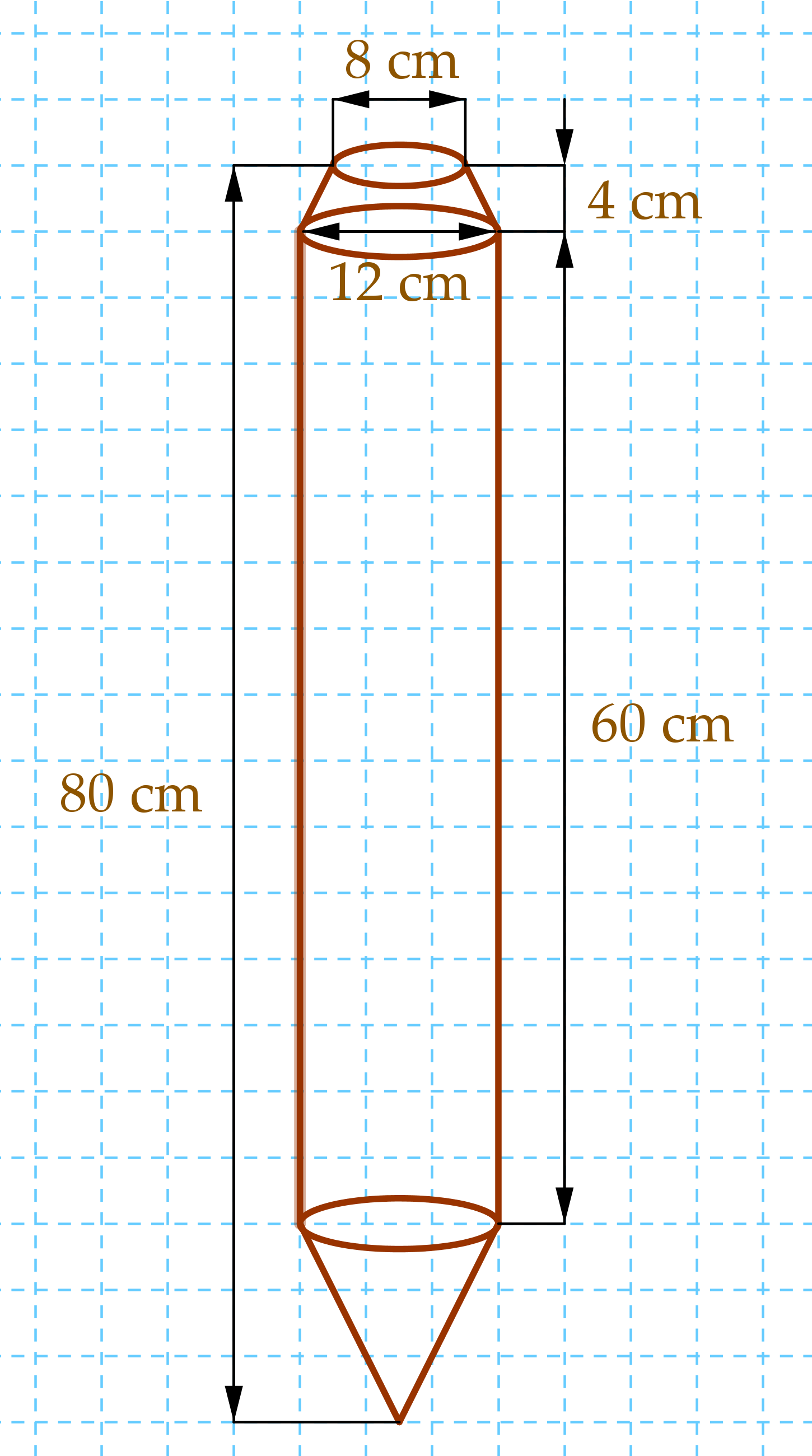
Mivel ezeknek a testeknek a felszíne és térfogata is kell,
felülről lefelé ezeket fogom kiszámolni.
1. Csonkakúp
Nagyítva kirajzolom a cölöp tetejét. A jelöléseket a
függvénytáblázat szerint használom.
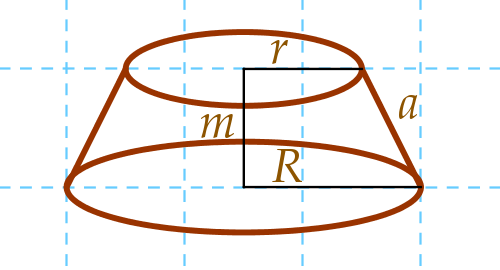
Mivel a feladatban a felső és az alsó kör átmérője van
megadva, ezért az r és R sugár
feleannyi: r = 8 : 2 = 4, R =
12 : 2 = 6.
Felsorolva az adatok:
- r = 4 cm
- R = 6 cm
- m = 4 cm
A felszín és térfogat képlete a függvénytáblázatból:
A felszín képletében szerepel az a, amit
ki kell számolni, a többi adat ismert. A számoláshoz a magasságot (m)
toljuk el a felső kör széléig. Így a jobb oldalon egy derékszögű
háromszög lesz:
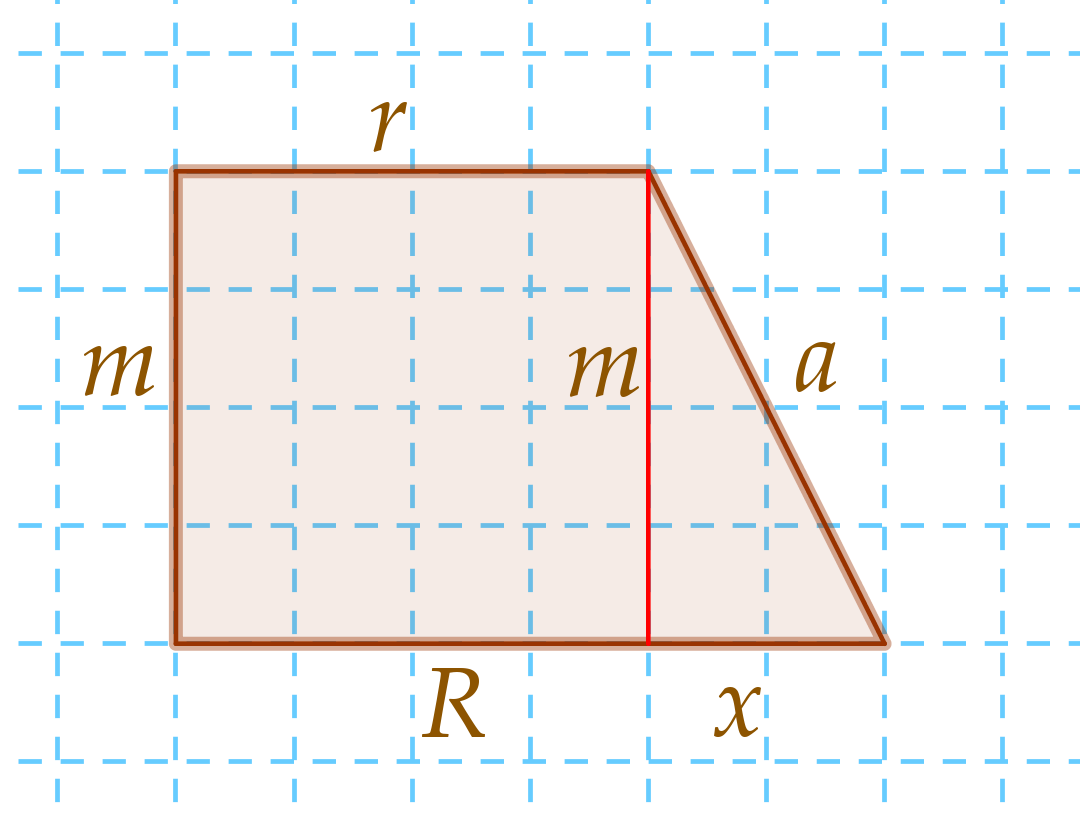
A háromszög alsó befogója (ami x-szel van
jelölve) a két sugár különbsége: x = R
- r = 6 - 4 = 2. Erre a háromszögre felírhatjuk a
Pitagorász-tételt:
m2 + x2 = a2
42 + 22 = a2
16 + 4 = a2
20 = a2 /√
4,47 = a
Így most már minden adatot ismerünk ahhoz, hogy
behelyettesítsük a képletekbe. Az eredmények:
- Acs = 303,79 cm2
- Vcs = 318,35 cm3
2. Henger
A henger felszínét és térfogatát is megkapjuk a
függvénytáblázatból:
A fentebbi ábráról leolvashatjuk az adatokat:
- r = 6 cm
- m = 60 cm
Itt most a kis r ugyanannyi, mint a
csonkakúpnál a nagy R, csak a függvénytáblázat
képlete szerint írtam. A képletben nincs más adat, ezért nem kell
plusszban kiszámolni semmit, csak behelyettesíteni a képletekbe. A
végeredmény:
- Ah = 2488,14 cm2
- Vh = 6785,84 cm3
3. Kúp
Végül a kúp következik. Ismét nagyítva a cölöp alját:
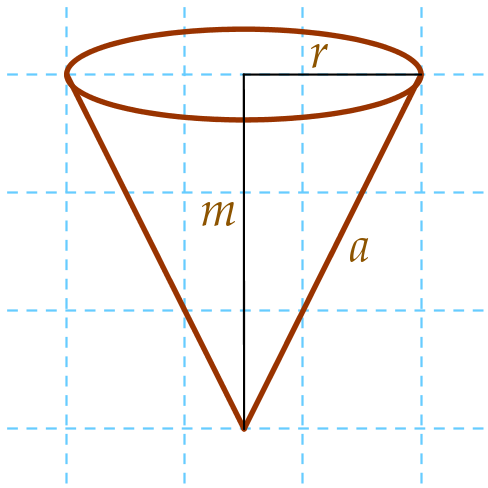
Most a kis r megintcsak ugyanannyi, mint
a csonkakúp alsó körének a nagy R-je, de a képletek
miatt lett kis r. A kúp magasságát úgy számolhatjuk
ki, hogy tudjuk, hogy a teljes cölöp 80 cm hosszú, ebből kivonjuk a
hengeres rész magasságát, meg a csonkakúp magasságát: 80 - 60 - 4 = 16
cm.
Az adatok:
- r = 6 cm
- m = 16 cm
A képletek:
Megint van egy hiányzó adat, mégpedig a kúp a
alkotója. Ezt kiszámíthatjuk Pitagorász-tétellel:
m2 + r2 = a2
162 + 62 = a2
256 + 36 = a2
292 = a2 /√
17,09 = a
Így megvan minden adat, ami a képletekbe kell. A végeredmény:
- Ak = 435,24 cm2
- Vk = 603,19 cm3
Ezek alapján mennyi lesz a cölöp felszíne és térfogata? Ha
összerakjuk a három alakzatot, akkor a felső csonkakúp alsó köre és a henger felső köre érintkezik, ezért ez a két kör kiesik a cölöp
felszínéből. Ugyanígy a henger alsó köre és a kúp köre is kiesik. Tehát a cölöp felszínét úgy kapjuk meg, hogy összeadjuk a három felszínt, de utána levonunk 4 körterületet (T0
):
Ac = Acs + Ah + Ak - 4 T0
Kör területet a következő képlettel számolunk: T0 = r2 π. Behelyettesítve r = 6-ot: T0 = 113,1 cm2
Ac = 303,79 +
2488,14 + 435,24 - 4 · 113,1 = 2775 cm2
A
térfogattal nincs olyan probléma, mint a felszínnél, a három térfogatot
csak simán össze kell adni:
Vc = Vcs + Vh + Vk = 318,35 + 6785,84 + 603,19 = 7707 cm3
Kiszámoltuk 1 cölöp felszínét és térfogatát, de a feladatban
5000 cölöp van. Ezért az előbb számolt értékeket még 5000-rel be kell
szorozni:
5000Ac = 13875000 cm2 = 1388 m2
5000Vc = 38535000 cm3 = 39 m3
A 39 m3 az 5000 db cölöp térfogata, de
a feladat nem ezt kérdezi, hanem azt, hogy mennyi fát használtak, ha a 18%-a hulladék. Ha a felhasznált fa 18%-a hulladék, akkor 82% nem
hulladék, hanem a cölöp. A kérdés az, hogy minek a 82%-a 39 m3?
A kérdéses fa mennyisége legyen x. Tehát x-nek
a 82% = 39. Azaz
x · 0,82 = 39
x = 39 : 0,82 = 48
Tehát 48 m3 fára volt szükség.
17. A Kis család 700 000 Ft megtakarított
pénzét éves lekötésű takarékban helyezte el az A
Bankban, kamatos kamatra. A pénz két évig kamatozott, évi 6%-os kamatos kamattal. (A kamatláb tehát ebben a bankban 6% volt.)
a) Legfeljebb mekkora összeget vehettek fel
a két év elteltével, ha a kamatláb a két év során nem változott?
A Nagy család a B Bankban 800 000 Ft-ot
helyezett el, szintén két évre, kamatos kamatra.
b) Hány százalékos volt a B
Bankban az első év folyamán a kamatláb, ha a bank ezt a kamatlábat a
második évre 3%-kal növelte, és így a második év végén a Nagy család
907 200 Ft-ot vehetett fel?
c) A Nagy család a bankból felvett 907 200
Ft-ért különféle tartós fogyasztási cikkeket vásárolt. Hány forintot
kellett volna fizetniük ugyanezekért a fogyasztási cikkekért két évvel korábban, ha a vásárolt termékek ára az eltelt két év során csak a 4%-os átlagos éves inflációnak megfelelően változott?
(A 4%-os átlagos éves infláció szemléletesen azt jelenti, hogy az előző
évben 100 Ft-ért vásárolt javakért idén 104 Ft-ot kell fizetni.)
Az első részt kétféleképpen oldhatjuk meg:
Vesszük a 700 000 Ft-ot, és kiszámoljuk, hogy az első év
végén mennyit kamatozik. A kamatláb 6%, tehát 6%-kal lesz több a pénz.
Ez azt jelenti, hogy a 700 000-nek a 106%-át kell venni: 700 000 · 1,06
= 742 000 Ft.
Ezután újabb egy év múlva megint 6%-kal lesz több, de most a
742 000 Ft-nak a 6%-ával. Ezért most a 742 000-t szorozzuk 1,06-tal:
742 000 · 1,06 = 786 520 Ft. Ezzel kész a megoldás.
A másik lehetőség, hogy a függvénytáblázatból kikeressük a
kamatos kamat számítást. Itt két képletet kell nézni:
Az egyikhez az van írva, hogy kamattényező:
$$ q =1+\frac {p}{100} $$ Itt p jelenti a kamatlábat, % nélkül, ami
a feladatban 6. Ha behelyettesítünk, akkor q-ra azt
kapjuk, hogy q = 1 + 0,06 = 1,06.
A másik képlet a kamatos kamattal felnövekedett tőke névre
hallgat: Tn = T0qn.
T0 az alaptőke,
amit a család betett a bankba. Ez 700 000 Ft: T0
= 700 000. n azt jelenti, hogy hány évre tették be
a pénzt: n = 2. A q pedig az,
amit az előbb kiszámoltam, tehát q = 1,06. Ezeket
behelyettesítve a képletbe:
T2 = 700 000 · 1,062
= 700 000 · 1,1236 = 786 520
Ugyanazt kaptam, mint az előbb.
A b) részben fordítva kell számolni, mint az előbb. Ennél a
kamatláb ismeretlen, jelöljük p-vel. A q
képletét módosítom úgy, hogy \$\frac{1}{100} $\ helyett 0,01-et írok:
q = (1 + 0,01 · p)
Az első évben tehát ezzel a q-val kell
szorozni a betett 800 000 Ft-ot.
1 év múlva a pénz: 800 000 · (1 + 0,01 · p)
A második évben már 3%-kal több a kamat. Ez azt jelenti, hogy p
helyett p + 3 van. Ebben az esetben q
= (1 + 0,01 · (p + 3))
Az első év végére kapott pénzt most ezzel kell még szorozni,
és így kapjuk meg a második év végére a 907 200 Ft-ot:
800 000 · (1 + 0,01 · p) · (1 + 0,01 · (p
+ 3)) = 907 200
Kaptunk egy ronda egyenletet, de legalább csak 1 ismeretlen
van benne. Osszunk le 800 000-rel, és a második zárójelben lévő belső
zárójelet bontsuk föl:
(1 + 0,01p) · (1 + 0,01p
+ 0,03) = 1,134
(1 + 0,01p) · (1,03 + 0,01p)
= 1,134
Most szorozzuk össze a két zárójeles tagot:
1,03 + 0,01p + 0,0103p +
0,0001p2 = 1,134
1,03 + 0,0203p + 0,0001p2
= 1,134
Ez egy másodfokú egyenlet, tehát 0-ra kell rendezni:
0,0001p2 + 0,0203p
- 0,104 = 0
Ha nem akarsz ilyen picike tizedestörtekkel számolni,
beszorozhatsz 10 000-rel:
p2 + 203p
- 1040 = 0
Így meg nagy számokat kaptunk, de hát ez van, a számológép
elbírja :-).
Megoldóképlettel megkapjuk a megoldást:
p1 = 5 és p2
= -208
A megoldás az 5% lesz, mert a másik megoldás negatív. (Ki
akarna negatív kamatra pénzt betenni?)
Próbáljuk értelmezni a c) feladatot. A család 907 200 Ft-ért
vásárolt cuccokat. Ugyanezek a cuccok 2 éve olcsóbbak volt, de az
infláció miatt drágábbak lettek. Mondjuk x Ft-ba
kerültek 2 éve. Egy év múlva már 4%-kal drágább volt, ami azt jelenti,
hogy 1,04-dal szorozni kell. Újabb egy év múlva még 4% a drágulás,
megint 1,04-dal szorozzuk. A végeredménynek pedig 907 200-nak kell
lennie. Egyenlettel:
x · 1,04 · 1,04 = 907 200
x = 838 757 Ft
Vajon így jól jártak? Hát persze, mivel 2 éve csak 800 000
Ft-juk volt, ami nem lett volna elég a 838 757 Ft-os cuccok
kifizetésére. De azt a 800 000 Ft-ot betették bankba, ami jobban
kamatozott, mint az infláció mértéke, így 2 év múlva már ki tudták
fizetni a termékeket.
18. Egy szerencsejáték a következőképpen
zajlik:
A játékos befizet 7 forintot, ezután a játékvezető feldob egy szabályos
dobókockát. A
dobás eredményének ismeretében a játékos abbahagyhatja a játékot; ez
esetben annyi
Ft-ot kap, amennyi a dobott szám volt.
Dönthet azonban úgy is, hogy nem kéri a dobott számnak megfelelő pénzt,
hanem
újabb 7 forintért még egy dobást kér. A játékvezető ekkor újra feldobja
a kockát. A két
dobás eredményének ismeretében annyi forintot fizet ki a játékosnak,
amennyi az első
és a második dobás eredményének szorzata. Ezzel a játék véget ér.
Zsófi úgy dönt, hogy ha 3-nál kisebb az első dobás eredménye, akkor
abbahagyja, különben pedig folytatja a játékot.
a) Mennyi annak a valószínűsége, hogy Zsófi
tovább játszik?
b) Zsófi játékának megkezdése előtt
számítsuk ki, mekkora valószínűséggel fizet majd neki a játékvezető
pontosan 12 forintot?
Barnabás úgy dönt, hogy mindenképpen két dobást kér majd. Áttekinti a
két dobás utáni
lehetséges egyenlegeket: a neki kifizetett és az általa befizetett pénz
különbségét.
c) Írja be a táblázat üres mezőibe a két
dobás utáni egyenlegeket!
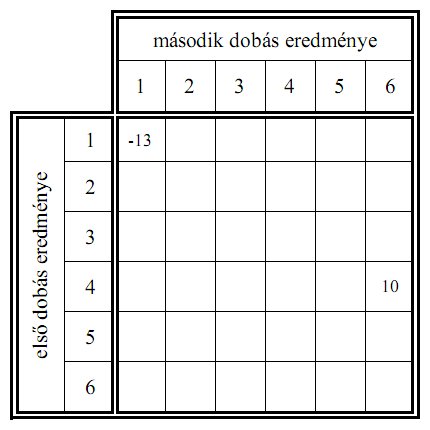
d)Mekkora annak a valószínűsége, hogy
Barnabás egy (két dobásból álló) játszmában nyer?
A 3. feladatnál megtudtuk, hogy a valószínűséget a
kedvezőperösszes szabállyal számoljuk ki. Az a) részt tehát úgy
kezdjük, hogy megnézzük, hány kedvező eset van. (Az összes eset nyilván
6, mert 1 kockával dob egyszer, a végeredmény 6 féle szám lehet.) Ha
Zsófi 3-nál kisebbet dob, abbahagyja. Ezért a továbbjátszáshoz 3-at,
vagy nagyobbat, azaz 4-et, 5-öt vagy 6-ot kell dobnia. Ez négy
lehetőség. Így a valószínűség: \$ \frac 46 $\=\$ \frac 23 $\. (Maradhat tört alakban, de az
se baj, ha átszámítjuk %-ra, de akkor végtelen tizedestörtet kapunk:
66,6%)
A b) részt kezdjük azzal, hogy az összes lehetőséget számoljuk
ki: az első dobás végeredménye 6-féle lehet, a második dobásé szintén
6-féle. Az összes lehetőség ezért 6 · 6 = 36.
A kedvező lehetőségekhez azt kell megnézni, mikor lesz két
szám szorzata 12. Ezt mutatja a táblázat:
| első dobás | Második dobás |
|---|---|
| 2 | 6 |
| 3 | 4 |
| 4 | 3 |
| 6 | 2 |
Viszont figyelembe kell venni azt is, hogy Zsófi nem játszik
tovább, ha az első dobás 2, ezért ezt a lehetőséget kihúzhatjuk. Így
marad 3.
Most már tudunk valószínűséget számolni: \$ \frac{3}{36} $\=\$ \frac{1}{12}$\. Kész. :-)
A c) feladatnál a táblázatot kell kitölteni. Mivel Barnabás
két dobást kér, ezért kétszer fizet 7 forintot, az 14 forint. A
kifizetett pénz pedig a két dobás szorzata. A táblázat tehát nem más,
mint egy szorzótábla, aminek minden értékéből 14-et ki kell vonni.
Például amit beírtak -13, az úgy jött ki, hogy 1-szer 1 az 1, ebből 14
az -13. A kitöltött táblázat:
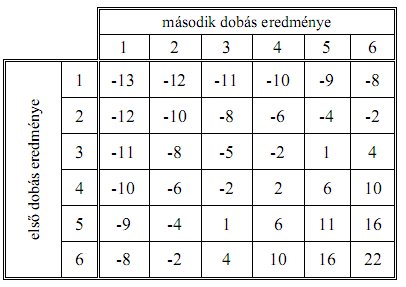
A táblázat kitöltése után a d) feladat sem okozhat problémát.
Meg kell számolni, hány kockába került pozitív szám. Ez lesz a kedvező
esetek száma. (Mondanom sem kell, hogy az összes eset 36.) Ha ügyesen
megszámoltuk, hogy 13 kockában van pozitív szám, akkor felírhatjuk,
hogy a valószínűség \$\frac{13}{36} $\.
