Tudja-e egy radioaktív atommag, hogy mikor kell elbomlania?
Ha van egy kupac radioaktív atommagom, akkor az úgy bomlik el, hogy valamennyi idő alatt a kupac fele elbomlik, a másik fele megmarad. Ezután a megmaradt atommagok fele szintén ugyanannyi idő alatt elbomlik. És így tovább. Ez az idő a felezési idő.
Konkrét példa: 1000 atommagom van, aminek 1 óra a felezési ideje. 1 óra múlva 500 atommagom marad, a többi elbomlik. 2 óra múlva 250. Tehát az 1. órában 500 atommag bomlott el, a másodikban 250, azaz kevesebb, mint az 1. órában. Ha folytatjuk a sort, a 3. órában már csak 125 atommag bomlik el. Egyre kevesebb atommag bomlik el! Az ember úgy érezné, hogy az atommagok tudják, hány atommag maradt, ennek megfelelő számú atommag bomlik csak el a következő órában. Pedig ez egyáltalán nincs így, az atommagoknak nem kell tudniuk egymás jelenlétéről.
Sőt, saját magunk is végezhetünk kísérletet. Vegyünk nagyon sok 5 forintost, rázzuk össze, és dobjuk az asztalra. Vegyük le az összes fejet, ami kb. a fele az összesnek. Az írásokkal ismételjük meg a rázást és a dobást. Megint vegyük le az összes fejet, ami most is kb. a fele a megmaradt pénzeknek. Ezt addig folytathatjuk, amíg nem marad egyetlen érme sem.
Tegyük fel, hogy az atommagokba be van programozva, hogy milyen valószínűség szerint bomoljanak el adott idő múlva. Ez a valószínűség olyan, hogy minél hosszabb idő telik el, annál nagyobb a valószínűsége, hogy most már elbomlik. Annak a valószínűsége, hogy egy T felezési idejű atommag t idő alatt elbomlik:
$$ p(t) = 1-2^{ -\frac{t}{T}} $$
Mit jelent ez a képlet? p-vel jelöljük a valószínűséget (angolul probability=valószínűség). Mivel időben változik a valószínűség, ezért az idő függvénye: p(t). Válasszuk a felezési időt 1 órának (T = 1 óra) és ábrázoljuk koordináta-rendszerben:
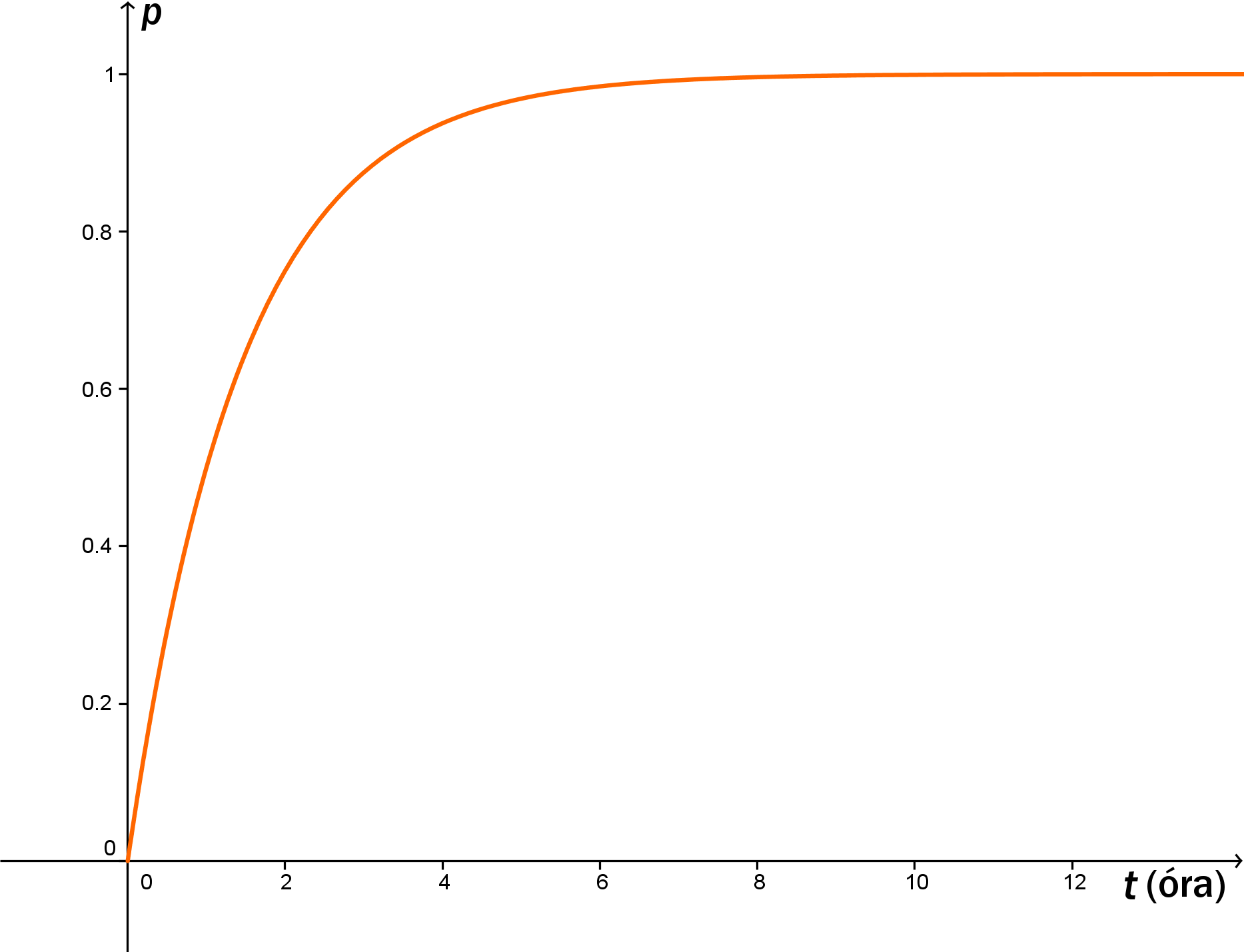
A vízszinte tengely mutatja az időt: ahogy telik, úgy nő a valószínűség. Kezdetben nagyon meredeken nő, viszont miután megközelítette az 1-et (100%-ot), belassul. Kb a felezési idő 8-szorosa után már 1-nek tekinthető, tehát tuti biztos, hogy elbomlik az atommag.
Most vegyünk n db atommagot, amik mind ugyanilyen valószínűség szerint bomlanak el. Kérdés, hogy mennyi a valószínűsége, hogy közülük k db elbomlik. Ezt binomiális eloszlással írhatjuk le:
$$ p_k =\binom{n}{k} \cdot p^k \cdot (1-p)^{n-k} $$
Az \$ \binom{n}{k} $\ (n alatt a k) azt jelenti, hogy hányféleképpen lehet n db különböző valami közül k db valamit kiválasztani. Például 10 különböző golyó van egy zsákban, belenyúlok, és kiveszek egyszerre 5-öt. Az összes lehetőség \$ \binom{10}{5} $\ = 252. Ismert példa a lottó kitöltésének összes lehetősége: itt 90 szám közül kell 5-öt beixelni. Ezt \$ \binom{90}{5} $\ = 43 949 268 féleképpen tehetjük meg. Az \$ \binom{1000}{500} $\ pedig egy irgalmatlanul nagy szám, 300 számjegyből áll.
Most a pk képletében a p helyébe írjuk az első egyenletet:
$$ p_k =\binom{n}{k} \cdot (1-2^{ -\frac{t}{T}})^k \cdot (2^{ -\frac{t}{T}})^{n-k} $$
Most jön a szép része a dolognak :). Mekkora a valószínűsége, hogy 1000 db, T=1 óra felezési idejű atommag közül 500 elbomlik? Azaz helyettesítsünk T helyére 1-et, n helyére 1000-et és k helyére 500-at. Egyedül t helyére nem írtunk számot, ezért a valószínűség függ az időtől. Ábrázoljuk a valószínűséget az idő függvényében.
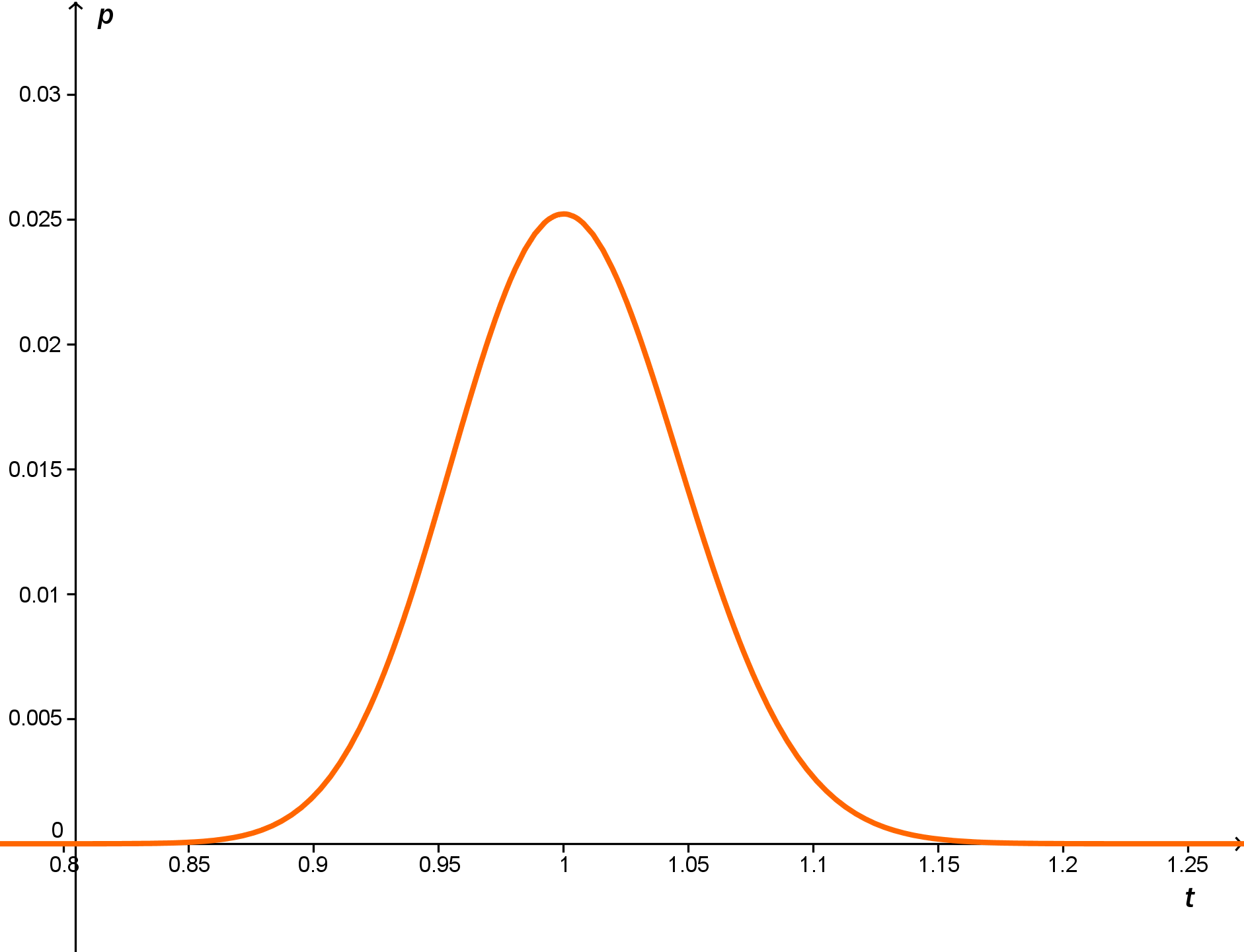
Láthatóan igen csekély a valószínűség, de pont 1 óránál maximális, kb 0,025=2,5 %. Hogyan lehetne nagyobb valószínűségeket kapni? Hát nem várhatom el az atommagoktól, hogy hajszál pontosan 1 óra alatt hajszál pontosan 500 bomoljon el (ez azt jelentené, hogy 1 óránál 100% a valószínűség). Nézzük meg, mennyi annak a valószínűsége, hogy 490 és 510 között lesz az elbomlott atommagok száma.
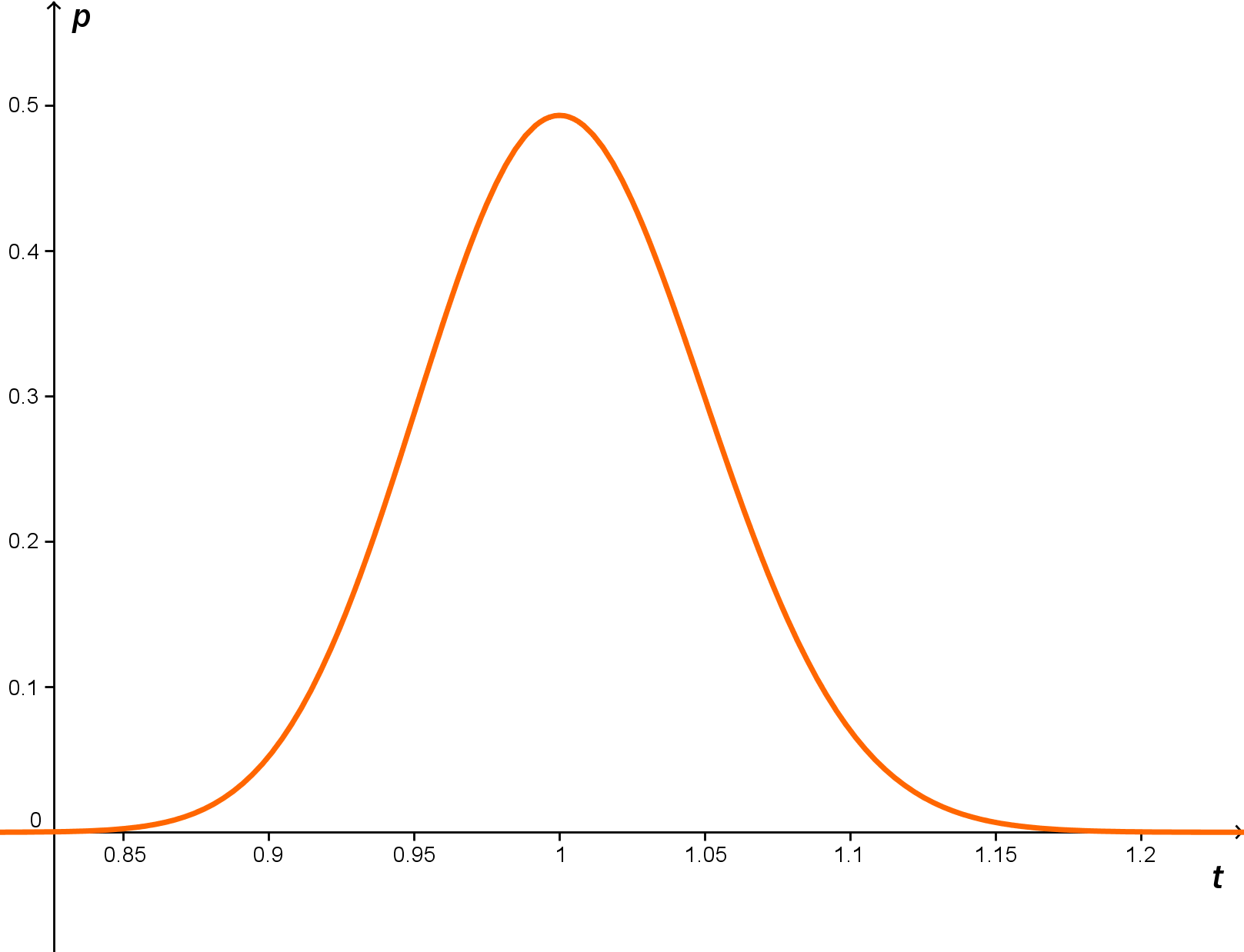
Na, erre már 50% esélyt kaptunk. Ez már elég jó. És még mindig 1 óránál van a maximum. Ha még nagyobb valószínűséget akarok kapni, akkor lehetne pl. 480 és 520 között az elbomlott atommagok száma (ekkor 80% lesz a maximum) stb.
De most inkább nézzük meg egy másik szemszögből a kérdést. Most rögzítsük le az időt. Legyen t=1 óra. Nézzük meg, mennyi a valószínűsége, hogy 1 óra alatt k db részecske bomlott el. (Tehát most az elbomlott részecskék függvényében nézem a valószínűséget.) Ekkor az eddigiekhez hasonló haranggörbét kapunk, aminek 500-nál van a maximuma, és ismét 2,5% a valószínűség. (Tehát annak a legnagyobb a valószínűsége, hogy 1 óra alatt 500 atommag bomlik el.)
Még valami, amit a valószínűségszámításból ismerünk: a várható érték. Megkérdezhetem, hogy várhatóan mennyi atom bomlik el adott idő alatt. A binomiális eloszlás várható értéke: np. Itt p helyére megint a p(t)-t kell írni. Ezt kapjuk:
$$ n \cdot (1-2^{ -\frac{t}{T}}) $$
Számoljuk ki, hogy a felezési idő alatt várhatóan hány atommag bomlik el (azaz amikor t=T).
$$ n \cdot (1-2^{ -\frac{T}{T}})= n \cdot (1-2^{ -1}) = $$ $$ = n \cdot (1-\frac 12) = n \cdot \frac 12 $$
Vagyis várhatóan az atommagok fele bomlik el a felezési idő alatt. Épp ezért hívják felezési időnek! :)
Egyetlen atommagról sosem fogjuk tudni megmondani, hogy pontosan mikor fog bomlani. Ugyanúgy egy feldobott pénzérméről sem tudjuk megmondani, hányadik dobásra lesz fej. Kizárólag valószínűségről beszélhetünk. Ezt a valószínűséget a kvantummechanikában ki is számolták. Az α-bomlást alagúteffektussal lehet leírni. Az alagúteffektus egy olyan jelenség, aminek következtében egy részecske képes átjutni egy magas fal túloldalára úgy, hogy nincs elég energiája átmászni rajta. Ezért úgy lehet elképzelni, mintha alagutat fúrt volna a falba, és azon ment volna át. Ugyanígy az atommagból az α-részecske alagutazással kiszabadul. Ennek valószínűsége adja az exponenciális bomlástörvényt.
A grafikonokat lehet ellenőrizni, más számadatokkal is kipróbálni a következő linkeken:
500 atom elbomlása
490-510 atom elbomlása
1 óra alatt elbomló atomok
