Hogyan oldjunk meg fizika érettségit?
Nézzük meg a 2009-es fizika középszintű érettségi megoldását!
Első rész
1. Ideális gáz izoterm állapotváltozás során 500 J munkát végez környezetén. Mekkora a gáz belsőenergia-változása?
A) A gáz belső energiája nem változik.
B) A gáz belső energiája 500 J-lal nő.
C) A gáz belső energiája 500 J-lal csökken.
Amikor izoterm állapotváltozásról van szó, akkor mindenki arra a képletre gondol, hogy p1V1=p2V2. Ez igaz is, de nem mond semmit a gáz belső energiaváltozásáról. Az első főtételből kell kiindulni: Δ Eb=Q+W. Egy gáz belső energiája a hőmérsékletével van kapcsolatban (tehát melegebb gáz belső energiája nagyobb), ezért a belső energia megváltozása a hőmérsékletét is megváltoztatja. Izoterm állapotváltozásnál nem változik a hőmérséklet, ebből kifolyólag a belső energia sem változik. Tehát a jó válasz az A.
2. Két különböző ellenállást kapcsoltunk össze. Milyen kapcsolásra lehet érvényes a következő állítás? Az eredő ellenállás kisebb, mint a kisebbik ellenállás.
A) Soros kapcsolásra.
B) Párhuzamos kapcsolásra.
C) Ilyen kapcsolás nem létezik.
Soros kapcsolásnál az eredő ellenállás a két ellenállás összege. Ami biztos, hogy nem lehet kisebb egyik ellenállásnál sem, mert nincs negatív ellenállás. Tehát az A válasz kilőve. A párhuzamos kapcsolás erdő ellenállását nehezebb kiszámolni: a két ellenállás reciprokát összeadjuk, majd az eredménynek vesszük a reciprokát. Ez fogas kérdés, hogy a végeredmény kisebb-e, mint a kisebbik ellenállás. Próbáljuk ki két konkrét értékkel: legyen 20 és 30. A reciprokuk összege \$ \frac{1}{12} $\, ennek a reciproka 12, ami kisebb, mint 20. Tehát párhuzamos kapcsolásra igaz az állítás, a jó válasz a B

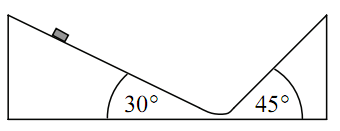
3. Egy kettős lejtő 30 fokos oldaláról kezdősebesség nélkül lecsúszik egy test. Milyen magasra jut fel a 45 fokos oldalon, ha a két lejtő közti átmenet zökkenőmentes és a súrlódás elhanyagolható?
A) Nem jut fel olyan magasra, mint amilyen magasról indult.
B) Ugyanolyan magasra jut fel, mint amilyen magasról indult.
C) Magasabbra jut fel, mint amilyen magasról indult.
Ilyen típusú feladatot legkönnyebben úgy oldhatunk meg, ha a test energiáját nézzük az egyes pontokban. A 30°-os lejtő tetején van helyzeti energiája: mgh (ha a lejtő magassága h). Ez az energia teljes egészében mozgási energiává alakul, amikor a lejtő aljára ér. Ezután ezzel az energiával indul felfelé a 45°-os lejtőn. A mozgási energia teljes egészében helyzeti energiává alakul, miközben eléri a legmagasabb pontot. Ha elfogy a mozgási energiája, akkor megáll. Mivel a mozgási energia ugyanannyi, mint a kezdeti helyzeti energia, most ez az érték újra helyzeti energia lesz a másik oldalon. De a helyzeti energia nem függ a megtett úttól, meg a lejtő hajlásszögétől sem, csak a magasságtól, ezért ezen az oldalon is h magasságig megy fel. Ezért a B válasz a helyes. Persze a valóságban mindig van súrlódás és légellenállás, ezért sosem megy fel ugyanolyan magasságra.
4. Egy adott kezdeti állapotú gáznak először állandó nyomáson, majd ugyanolyan kezdőállapotból kiindulva állandó hőmérsékleten csökkentjük a térfogatát 1 dm3-rel.
Melyik esetben végzünk több munkát?
A) Akkor, amikor a nyomás állandó.
B) Akkor, amikor a hőmérséklet állandó.
C) Pontosan egyforma a munkavégzés a két esetben.
Ha gázon munkát végzünk, akkor a pV diagramot kell használni. Ezen ugyanis a végzett munka a görbe alatti terület:
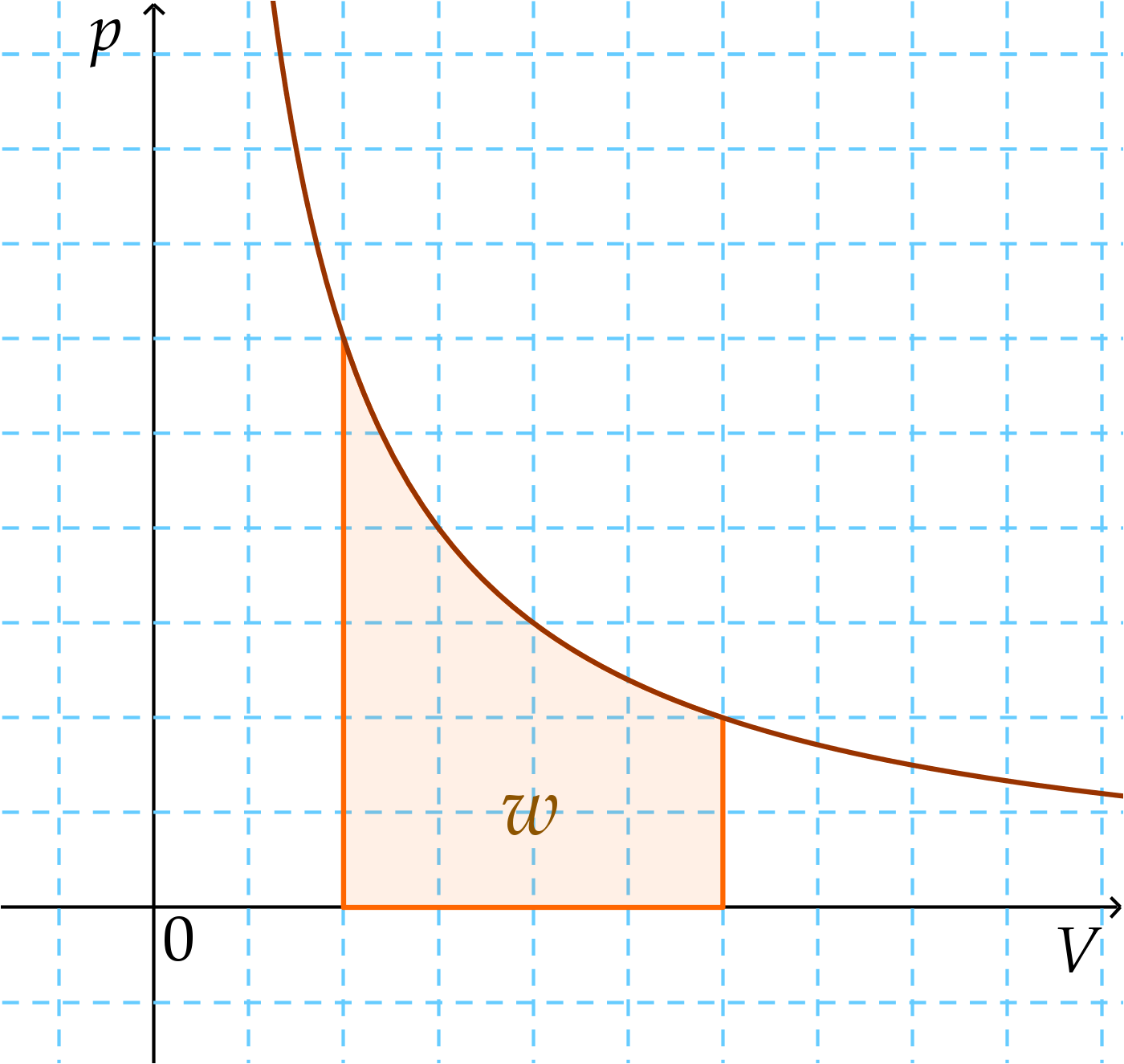
Az ábrán a görbe egy izoterma (azaz olyan állapotváltozás, amikor a hőmérséklet nem változik). A beszínezett terület a végzett munka. De nézzük a feladatot. Az első állapotváltozás olyan, hogy állandó nyomáson csökkentjük a térfogatát. Ez grafikonon így néz ki:
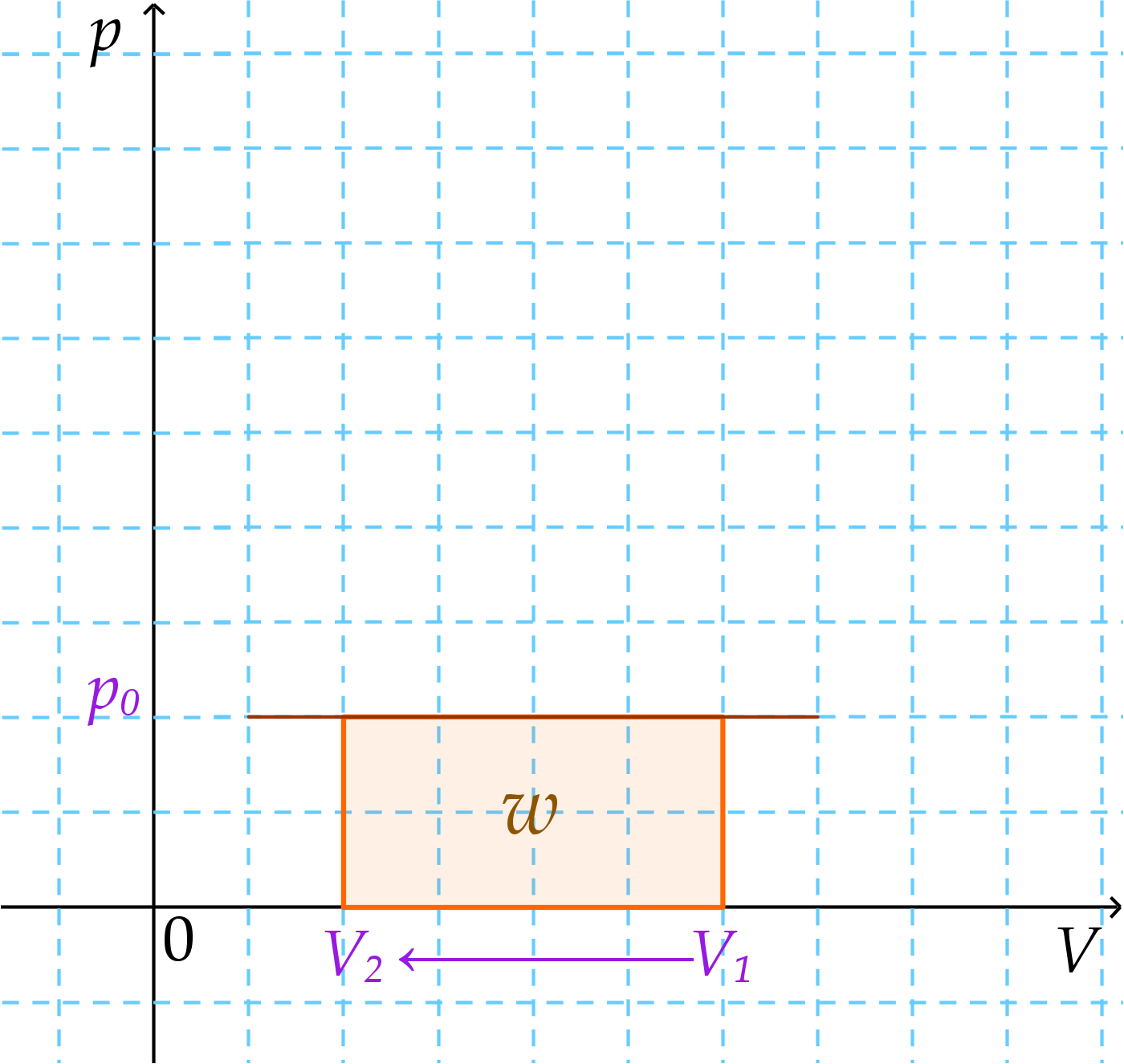
A másik pedig egy állandó hőmérsékleten végzett állapotváltozás. Ugyanabból a kezdő állapotból indulunk ki, de most a nyomás változhat, a hőmérséklet nem. Az ennek megfelelő grafikon ugyanolyan izoterma, mint az első ábrán.
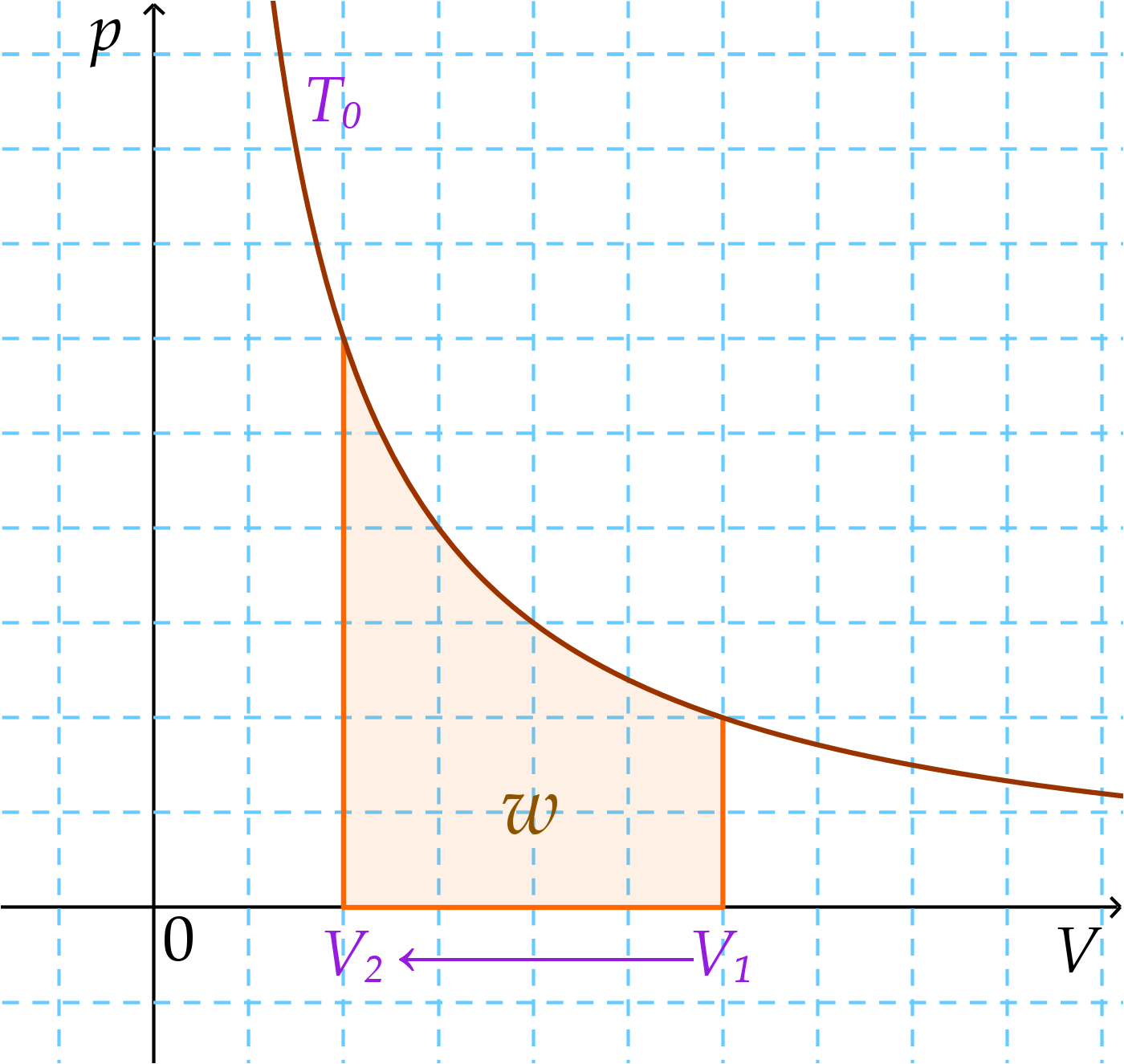
Ránézésre összehasonlítva látható, hogy az utolsó ábrán nagyobb a végzett munka, mint az állandó nyomás esetében. Ezért a jó válasz a B.
5. Egy 0,1 kg-os tömegű test súrlódásmentesen lecsúszik egy
félgömb alakú gödörbe. Mit állíthatunk a nyomóerőről, amikor a test a gödör legalsó pontján halad át? (g = 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\ )
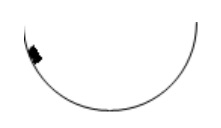
A) A nyomóerő kisebb, mint 1 N.
B) A nyomóerő éppen 1 N.
C) A nyomóerő nagyobb, mint 1 N.
Mennyi lenne a nyomóerő, ha a test nem mozogna, hanem csak állna a talajon? A nyomóerő a testre lefelé ható erőket egyensúlyozza ki. Ha a test csak áll, akkor az egyetlen lefelé ható erő a gravitációs erő, ami mg = 0,1 kg ⋅ 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\ = 1 N. Ugyanennyi a nyomóerő értéke is, mert a test egyensúlyban van, és két egymást kioltó erő nagysága megegyezik.
Mi változik, ha a test mozog, jelen esetben félkör alakú pályán? Körmozgásnál a testre centrifugális erő is hat. Gondolj a mosógépre: centrifugázásnál a víz kipréselődik a ruhából. Ezért amikor a test a gödör alján halad át, lefelé két erő hat: a gravitációs (ugyanúgy, mint az álló esetben), és a centrifugális. Ez a két erő összességében nagyobb, mint 1 N, ezért a felfelé ható nyomóerő is nagyobb, mint 1 N. Tehát a helyes válasz a C
6. Három különböző tömegű részecskét tömegük szerint növekvő sorrendbe szeretnénk állítani. Melyik a helyes sorrend?
A) Elektron, neutron, proton.
B) Elektron, proton, neutron.
C) Proton, elektron, neutron.
A függvénytáblázatból egyszerűen ki lehet keresni a részecskék tömegét.
| elektron: | 9,109 3879 ⋅ 10-31 kg |
| neutron: | 1,674 9286 ⋅ 10-27 kg |
| proton: | 1,672 6231 ⋅ 10-27 kg |
Ebből már látszik, hogy a helyes sorrend a B.
Hogyan lehetett volna máshogy kitalálni a megoldást? Azt illik tudni, hogy az elektron tömege pici, a proton tömegének 1837-ed része. Azt is tudhatod, hogy a proton és a neutron tömege nagyjából megegyezik. De melyik nagyobb és miért? Atomfizikából tanultad, hogy a neutron el tud bomlani egy protonra, egy elektronra és egy antineutrínóra. Ebből következik, hogy a neutron tömege nagyobb, mint a protoné.

7. Hőszigetelt edényben lévő 0 °C-os vízbe 0 °C-os jeget teszünk. Változik-e a víz tömege néhány perc elteltével?
A) Igen, a víz tömege nő.
B) Igen, a víz tömege csökken.
C) Nem, a víz tömege nem változik.
Mi történhet, amitől megváltozik a víz tömege? Vagy a jég olvad el, vagy a víz fagy meg. Ha a víz is meg a jég is 0 °C-os, akkor azok hőmérsékleti (vagy termikus) egyensúlyban vannak, ebben az esetben viszont nem történik semmi, a jég jég marad, a víz meg víz. Ezért a helyes válasz a C.
Lehet, hogy egy kicsit túlzás azt mondani, hogy nem történik semmi. Valójában a jégből mindig elolvad egy kicsi, a vízből pedig megfagy egy kicsi, de ez a két mennyiség ugyanannyi, ezért nem érzékelünk változást.

8. Lehet-e egy áramjárta egyenes tekercset iránytűként felhasználni?
A) Igen, de csak akkor, ha a tekercs felfüggesztése olyan, hogy az elég könnyen elfordulhat.
B) Nem, mivel iránytűnek csak permanensen mágnesezett anyag használható.
C) Igen, de csak akkor, ha nem helyezünk bele vasmagot.
Az iránytű beáll a Föld mágneses mezőjének irányába. Ezt akkor fogja megtenni, ha maga is mágneses. Kérdés, hogy egy áramjárta tekercsnek van-e mágneses mezője? A válasz az, hogy van. Tehát a két igen válasz közül kell választani. Változtat-e a tekercs mágnesességén a vasmag? Hát persze, attól erősebb lesz. Tehát ha vasmagot teszünk bele, az még előnyös is lehet. Tehát C kizárva. Ezért az A válasz lesz a jó, mert tényleg fontos, hogy könnyen elfordulhasson a tekercs. (Az iránytű tűje is könnyen elfordul.)
9. Egy 50 cm hosszú rugót egy 2 kg tömegű test 20 cm-rel nyújt meg, ha ráakasztjuk.
Mennyire nyújtaná meg egy 2 kg tömegű test ugyanezen rugónak egy 25 cm-es
darabját?
A) 10 cm
B) 20 cm
C) 40 cm
A rugó megnyúlása egyenesen arányos a hosszával. Ebből már következik, hogy fele akkora rugó fele annyit nyúlik meg. Tehát az A válasz a jó.
Mondjuk ha nem tudjuk, hogy egyenes arányosság van, akkor hogy lehetett volna kikövetkeztetni? Képzeljuk el, hogy mi van akkor, ha a B vagy C a jó válasz, tehát a rövidebb rugó vagy ugyanannyit nyúlik meg, vagy jobban. Vegyük a rugónak nem a felét, hanem sokkal kisebb darabját, mondjuk csak 1 cm-t. Ha ez az 1 cm-s darab 20 cm-t nyúlna, akkor valószínűleg elszakadna, mert a rugó kicsavarodik, és egy vasdrótot kapunk, amit még tovább kéne nyújtani. Ehhez viszont érezhetően nagyobb erő kéne.
10. A hidrogénatom elektronjának energiaszintjeit a Bohr-modell szerint az En = -2,2 \$ \frac{\mathrm{aJ}}{n^2} $\ összefüggés adja meg. Mekkora energiát bocsát ki a hidrogénatom, ha elektronja az első gerjesztett energiaszintről a legmélyebb energiaszintre ugrik?
A) 2,2 aJ
B) 1,65 aJ
C) 0,55 aJ
Adva van egy képlet, amiben n változik, mégpedig 1-től kezdve egész értékeket vehet fel. Honnan lehet tudni? Mert benne van a kérdésben, hogy első gerjesztett szint. Ebből következik, hogy van második, harmadik, ennedik szint, ami nem lehet tört. (De 0 sem lehet, mert akkor 0-val kéne osztani.) Mennyi lehet a legmélyebb szint? Kezdjük el n helyére beírni a számokat:
| n=1 | E1 = -2,2 \$ \frac{\mathrm{aJ}}{1^2} $\ = -2,2 aJ |
| n=2 | E2 = -2,2 \$ \frac{\mathrm{aJ}}{2^2} $\ = -\$\frac{2,2}{4} $\ aJ = -0,55 aJ |
| n=3 | E3 = -2,2 \$ \frac{\mathrm{aJ}}{3^2} $\ = -\$\frac{2,2}{9} $\ aJ = -0,244 aJ |
A legmélyebb szint tehát a -2,2 aJ, mert a többi érték ennél nagyobb. Ez a szint az alapállapot. Az ennél eggyel nagyobb szint az első gerjesztett állapot, és így tovább. A kérdés ezek szerint az, hogy az E2-ről E1 szintre ugorva mennyi az energiakülönbség? A táblázatból vett adatokból: -0,55 - (-2,2) = 1,65 aJ. Ez pedig a B válasz.
11. Egy síktükröt pontszerű fényforrással világítunk meg. Mit mondhatunk a fényforrásból kiinduló sugarakról a tükörről való visszaverődés után?
A) Összetartanak.
B) Párhuzamosak.
C) Széttartanak.
Kezdjük azzal, hogy a pontszerű fényforrásból induló sugarak mit csinálnak? Minden irányban szétterjednek, tehát széttartanak. Síktükörbe már mindenki nézett: saját magát látja torzítatlanul. Nyílván a fényforrás tükörképe is torzítatlan, tehát a tükörképből induló fénysugarak is széttartanak. Ezért a jó válasz a C.
Azt azért hozzá kell tenni, hogy a fény nem a tükörképből jön, hanem a tükör felületéről verődik vissza, de pont úgy, mintha a tükör mögötti fényforrásból jönne.
12. Az alábbi sugárzások közül melyik nem elektromágneses hullám?
A) Az alfa-sugárzás.
B) Az ultraibolya sugárzás.
C) A gamma-sugárzás.
Ezeket a sugárzásokat ismerni kell, de a függvénytáblázat most is segít. Az elektromágneses sugárzások típusai táblázatban szerepelnek. Az ultraibolya és a gamma-sugárzás is benne van. Marad az alfa-sugárzás, ami pedig a hélium atommagját tartalmazza, ez tehát nem elektromágneses sugárzás. A helyes válasz: A.
13. Egy radioaktív anyag felezési ideje 1 óra. Hányad része bomlik el az anyagnak 3 óra alatt?
A) \$ \frac{1}{8}$\
B) \$ \frac{5}{6} $\
C) \$ \frac{7}{8} $\
Ha a felezési idő 1 óra, akkor minden órában megfeleződik a még el nem bomlott atomok száma. 3 óra alatt 3-szor feleződik, tehát a nyolcada marad elbomlatlan. Ebből következik, hogy a \$ \frac{7}{8} $\-a elbomlik. A jó válasz a C.
14. Három fényforrásunk van: egy 1 W-os, egy 1,5 W-os és egy 2 W-os. Ezek segítségével egyesével fényelektromos jelenséget szeretnénk létrehozni. A következőket tudjuk: Az 1 W-os fényforrás nem vált ki a vizsgált fémből fényelektromos jelenséget. A 1,5 W-os fényforrás kiváltja a jelenséget. A 2 W-os fényforrás az 1 W-os fényforrással megegyező frekvenciájú fényt bocsát ki. Mit állíthatunk a 2 W-os fényforrásról?
A) A 2 W-os fényforrás biztosan kiváltja a fényelektromos jelenséget.
B) Lehet, hogy a 2 W-os fényforrás kiváltja a fényelektromos jelenséget.
C) A 2 W-os fényforrás biztosan nem váltja ki a fényelektromos jelenséget.
A fényelektromos jelenségnek az a lényege, hogy egy foton kilök egy elektront a fémből. Ehhez a foton energiájának legalább annyinak kell lenni, mint az elektron kötési energiája. A foton energiája viszont a frekvenciájától függ. Miben különbözik egy 1 W-os és egy 2 W-os izzó? A 2 W-os fényesebb, azaz több fotont sugároz szét. De ha az 1 W-os és a 2 W-os izzó azonos frekvenciájú fotonokat bocsát ki, akkor az egyes fotonok energiája mindkét esetben ugyanannyi. Ha az 1 w-os nem vált ki fotoeffektust, akkor a 2 W-os sem fog. Itt nem igaz az, hogy sok lúd disznót győz: egy elektront egy foton tud kilökni, és ha egy fotonnak ehhez kicsi az energiája, akkor nincs fotoeffektus, akkor sem, ha több foton "támad". Ezért a jó válasz a C.
15. Az alábbi tudósok közül melyik ismerte fel a láncreakció lehetőségét?
A) Teller Ede.
B) Szilárd Leó.
C) Wigner Jenő.
Ez tudománytörténeti dolog, tehát valaki vagy tudja, vagy nem. A helyes válasz B. Érdekességként leírom, hogy miután Szilárd Leó rájött a láncreakció lehetőségére, Einsteinnel levelet írt Roosevelt elnöknek, amiben kifejtik, milyen pusztító lehet egy atombomba.

Albert Einstein és Szilárd Leó a Roosevelt elnöknek írt levél fogalmazásakor.
16. Hány \$ \frac{\mathrm{km}}{\mathrm{h}} $\-nak felel meg 36 \$ \frac {\mathrm{m}}{\mathrm{s}} $\?
A) 129,6 \$ \frac{\mathrm{km}}{\mathrm{h}} $\
B) 36 \$ \frac{\mathrm{km}}{\mathrm{h}} $\
C) 10 \$ \frac{\mathrm{km}}{\mathrm{h}} $\
Ez csak egy egyszerű (?) mértékegységátváltás. \$ \frac {\mathrm{m}}{\mathrm{s}} $\-ról hogyan váltunk át \$ \frac{\mathrm{km}}{\mathrm{h}} $\ -ra? Szorozni kell 3,6-del. 36 · 3,6 = 129,6. Ez pedig az A válasz. A becsapás abban van, hogy 36-ot 3,6-del osztani könnyebb, így a C válasz csábítóbb.
17. Fel tud-e mágnesezni egy közönséges mágnes egy acéldarabot?
A) Nem, mert a mágnesnek két pólusa van, és azok szétválaszthatatlanok.
B) Igen, de csak akkor, ha hozzáérintjük.
C) Igen, akár hozzáérintjük, akár a közelébe helyezzük.
A mágnesnek mágneses mezeje van, de nem csak a mágnes anyagában, hanem azon kívül is. Ez a mágneses mező lép kölcsönhatásba a környező anyagokkal (leginkább vassal). Az acél könnyen mágnesezhető. De mi mágnesezi fel az acélt? A mágneses mező. Ezért a mágnesnek nem kell érintkeznie az acéllal, elég ha ezt megteszi a mágneses mező. Persze ehhez az acélt közel kell tenni a mágneshez, mert csak ott elég nagy a mágneses mező. A helyes válasz tehát a C.
18. A grafikon egy egyenes vonalú mozgást végző test pillanatnyi sebességének nagyságát mutatja az idő függvényében. Az alábbi jelenségek közül melyikre vonatkozhat a grafikon?
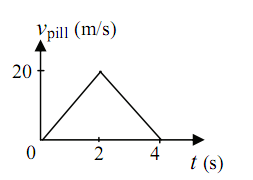
A) Egy feldobott kő eléri pályája tetejét, visszafordul, földet ér, és megáll.
B) Egy rugón rezgő test az egyik, illetve másik szélső helyzete között mozog.
C) Egy autó elindul, felgyorsul, majd lefékez és megáll.
Vegyük sorra a válaszokat!
A) Ha feldobunk egy követ, akkor kezdősebességet adunk neki. Mivel a Föld húzza lefelé, ezért lassul, és valahol magasan megáll, itt 0 a sebessége. Ezután visszaesik, és most gyorsul, egyre nagyobb a sebessége, amíg be nem csapódik a földbe. Ekkor a sebessége rövid idő alatt 0-ra esik.
B) A rugóra függesztett test harmonikus rezgőmozgást végez. Ennek a mozgásnak a görbéje szinuszos jellegű.
C) Az autó elindul (nyilván 0 sebességről), gyorsít, elér egy bizonyos sebességet, majd a fékre tapos a vezető, és elkezd lassulni, amíg meg nem áll, azaz újra 0 lesz a sebessége.
Ezekből remélhetőleg kitalálható, hogy a C a jó válasz.
19. Hatnak-e a Nap körül keringő bolygók gravitációs vonzerővel a Napra?
A) Igen, de a Nap mozgására gyakorolt hatásuk annak nagy tömege miatt elhanyagolható.
B) Nem, hiszen akkor a Nap nem lehetne nyugalomban.
C) Igen, ezért mozog a Nap a Tejútrendszeren belül a Herkules csillagkép felé.
Newton szerint két tömeggel rendelkező test kölcsönösen vonzzák egymást. Tehát nem lehet, hogy csak az egyik vonzza a másikat. Ezzel a B választ kilőttük. Most már csak azt kell tudni, miért mozog a Nap a Herkuls csillagkép felé. Bármi is az oka, a Nap magával viszi a bolygókat is. Tehát ez a hatás együtt hat az egész Naprendszerre. Ráadásul a bolygók a Nap körül össze-vissza helyezkednek el, az egyik erre húzná, a másik arra, ezek a vonzások kiejtik egymást. Marad az A.

20. Két testet termikus kölcsönhatásba hozunk. Az egyik test („A”) belső energiája 30 J, a másiké („B”) 50 J. Melyik test ad le és melyik test vesz fel energiát a kölcsönhatás során?
A) A „B” test ad át energiát az „A”-nak, mert kezdetben a „B”-nek nagyobb az energiája.
B) Az „A” test ad át energiát a „B”-nek, mert kezdetben az „A”-nak nagyobb a hőmérséklete.
C) A megadott adatok alapján nem dönthető el a kérdés.
Mikor jön létre termikus kölcsönhatás két test között? Ha különbözik a hőmérsékletük. Ilyenkor mindig a melegebb ad le energiát a hidegebbnek. El lehet dönteni egy test belső energiájából, hogy mennyi a hőmérséklete? Nem, mert kéne azt is tudni, milyen anyagból van, mennyi a tömege, stb. Erről nincs infó, tehát nem eldönthető, ezért a C válasz a helyes.
Második rész
1. Az ábrán látható elrendezésben két testet helyezünk egy kétkarú mérleg két karjára, és az egyikhez csigán átvetett fonalat erősítünk.
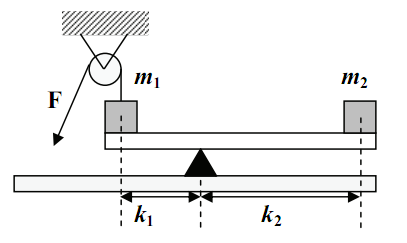
A mérleg karja súlytalannak tekinthető!
Adatok: m1 = 10 kg, m2 = 2 kg,
k1 = 1 m, k2 = 2,5 m, g = 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\
a) Mekkora F erővel kell húznunk a fonalat, hogy a rendszer egyensúlyban legyen?
b) Hová kell tennünk az m2 testet, hogy F = 75 N erő legyen szükséges az egyensúly fenntartásához?
A kétkarú mérleges feladatokat forgatonyomatékkal lehet legkönnyebben megoldani. Mi a forgatónyomaték? Erő szorozva erőkarral. Milyen erők vannak az ábrán? A kérdéses F erő nyilván. Továbbá még a két doboz súlya. (Ugyebár a súly az az erő, amivel a test nyomja az alátámasztást. Az alátámasztás most a mérleg karja.) A súlyt úgy számoljuk ki, hogy a tömeget szorozzuk g-vel (nem véletlenül adták meg az adatok között). Legyen F1 és F2 az 1-es és 2-es test súlya. A keresett F erő az 1-es testhez kötött kötélen keresztül fejti ki a hatását. Ez az erő tulajdonképpen az 1-es test súlyát csökkenti.
Mivel a mérleg egyensúlyban van, ezért a forgatónyomatékok összegének 0-nak kell lennie. Figyelembe kell venni, hogy a forgatónyomaték pozitív és negatív is lehet. (Akkor pozitív, ha az óramutató járásával ellentétes irányban forgat.) Ezen kívül még egy pontot is ki kell jelölni, ami körül forog a mérleg karja. Ez a pont legyen a fekete háromszög csúcsa. Ekkor az 1-es test pozitív, a 2-es negatív irányban forgat. Tehát az egyenletünk:
(F1 - F) ⋅ k1 - F2 ⋅ k2 = 0
F1 - F azt fejezi ki, hogy az 1-es test súlyát az F erővel csökkentjük. Most helyettesítsük be az egyenletbe az ismert adatokat:
(10 kg ⋅ 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\ - F) ⋅ 1 m - 2 kg ⋅ 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\ ⋅ 2,5 m = 0
Itt az F1 helyére m1 ⋅ g-t írtam, meg hasonlóan F2-re is. Számoljuk ki amit tudunk, és bontsuk fel a zárójelet:
100 - F - 50 = 0
Ebből már könnyen látszik, hogy F = 50 N. (A számolásnál nem írtam mértékegységeket, de a végén ki kell írni, hogy N.)
A b feladathoz ugyanazt az egyenletet kell felírni a forgatónyomatékokra, mint az előbb, de most más az ismertlen. A 2-es test új helyzetében az erőkar legyen k2', F helyére pedig 75 N-t kell helyettesíteni, a többi marad. Ezt kapjuk:
(10 kg ⋅ 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\ - 75 N) ⋅ 1 m - 2 kg ⋅ 10 \$ \frac{\mathrm{m}}{\mathrm{s}^2} $\ ⋅ k2' = 0
25 - 20 ⋅ k2' = 0
k2' = 1,25 m.
Ezzel kész is a feladat.
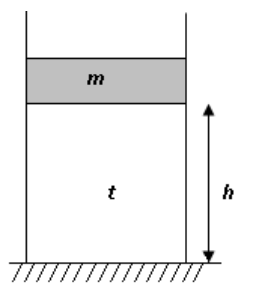
2. Az ábrán látható függőleges hengerben egy súrlódás nélkül mozgó dugattyú levegőt zár be. A dugattyú tömege m = 10 kg, felülete A = 20 cm2, a levegőoszlop magassága h = 10 cm, hőmérséklete
t = 20 °C,
a külső légnyomás 105 Pa.
Mekkora a bezárt levegő sűrűsége és tömege?
(A megoldás során akár a levegő normálállapothoz tartozó sűrűsége ρ0 = 1,29 \$ \frac{\mathrm{kg}}{\mathrm{m}^3} $\, akár a levegő átlagos moláris tömege M = 29 \$ \frac{\mathrm{g}}{\mathrm{mol}} $\ felhasználható.)
Gondoljuk végig, mi kell ahhoz, hogy meghatározzuk a gáz tömegét. Használjuk a gázok állapotegyenletét:
p⋅V = n⋅R⋅T
p a gáz nyomása, V a térfogata, n az anyagmennyiség, T a hőmérséklet, R pedig az univerzális gázállandó, R = 8,314 \$ \frac{\mathrm{J}}{\mathrm{kg K}} $\. Tök jó ez a képlet, de nincs benne a tömeg, amit kérdeznek. De benne van az anyagmennyiség, abból viszont már tudunk tömeget számolni. Megadták a moláris tömeget, ami megadja 1 mol anyag tömegét. Ha kiszámoljuk n-et, akkor a tömeget is ki tudjuk számolni: m=M⋅n.
Nézzük meg, mit tudunk a gáztörvényből: a térfogatot ki tudjuk számolni (henger térfogat): alapterület szorozva magassággal.
V = A ⋅h = 20 cm2 ⋅ 10 cm = 200 cm3 = 0,0002 m3
A hőmérséklet simán meg van adva: t = 20 °C,
amit át kell váltani kelvinbe: T = 293 K
Most már csak a nyomás hiányzik. Mi nyomja a gázt felülről? Egyrészt a levegő p0 = 105 Pa nyomással. Másrészt a 10 kg-os dugattyú. Ennek a nyomását úgy számoljuk ki, hogy a dugattyú súlyát osztjuk a felülettel: $$ p = \frac{F}{A}=\frac{mg}{A}=\frac{10\mathrm{kg}\cdot 10\frac{\mathrm{m}}{\mathrm{s}^2}}{0,002\mathrm{m}^2}=50000\mathrm{Pa} $$
Az össznyomás a légnyomás és a dugattyú nyomásának összege:
p = 105 Pa + 50000 Pa = 150000 Pa.
Most már mident ismerünk a képletben, csak n-et nem, de ezt ki tudjuk számolni:
150000 Pa ⋅ 0,0002 m3 = n ⋅8,314\$ \frac{\mathrm{J}}{\mathrm{kg K}} $\ ⋅ 293 K
30 = n ⋅ 2436
n = 0,0123 mol
Végül a tömeget is megkapjuk:
m= 29 \$ \frac{\mathrm{g}}{\mathrm{mol}} $\ ⋅ 0,0123 mol = 0,357 g.
Ezzel kész a feladat.
Nézzük meg, hogy a másik megadott adattal, a levegő sűrűségével hogy lehetett volna kiszámolni. Normál állapothoz tartozó sűrűséget adtak meg, ami azt jelenti, hogy a nyomás 105 Pa, a hőmérséklet pedig 0 °C. A sűrűséget úgy számítjuk ki, hogy ρ = \$ \frac mV $\. Ebből V = \$ \frac{m}{\rho} $\. (A p-nek kinéző betű valójában ró.)
Ismerjük az egyesített gáztörvényt: $$ \frac{p_1 V_1}{T_1}=\frac{p_2 V_2}{T_2} $$
Helyettesítsük be V helyére az \$ \frac{m}{\rho} $\-t: $$ \frac{p_1 m_1}{T_1 \rho_1}=\frac{p_2 m_2}{T_2 \rho_2} $$
A bezárt gáz tömege nem változik, m1 = m2, ezért egyszerűsíthetünk vele: $$ \frac{p_1}{T_1 \rho_1}=\frac{p_2}{T_2 \rho_2} $$
Az egyenlet bal oldalára beírjuk a normál állapothoz tartozó értékeket, a jobb oldalra pedig a feladat szerinti értékeket: $$ \frac{10^5}{273 \cdot 1,29}=\frac{1,5 \cdot 10^5}{293 \cdot \rho_2} $$
Ebből ρ-t ki tudjuk számolni: ρ = 1,803 \$ \frac{\mathrm{kg}}{\mathrm{m}^3} $\ = 0,0018 \$ \frac{\mathrm{g}}{\mathrm{cm}^3} $\. A tömeget úgy kapjuk meg, hogy m = ρ⋅V = 0,0018 \$ \frac{\mathrm{g}}{\mathrm{cm}^3} $\ ⋅ 200 cm3 = 0,36 g. Ez egyezik az előző számolással (ha kerekítünk).
3/A Egy 10 W-os, hálózati feszültségre méretezett egyszerű izzólámpának lágy és viszonylag hosszú wolframszálból készül az izzószála. Ha működés közben egy erős mágnes egyik pólusát közelítjük az üvegburához, akkor azt tapasztaljuk, hogy az izzószál heves rezgésbe jön.
a) Miért jön rezgésbe az izzószál?
b) Hosszabb idő (néhány perc) elteltével megállapodik-e valahol az izzószál?
c) Mi állítható az izzószálra ható erőről, ha a hálózati feszültség helyett egyenfeszültséggel üzemeltetjük az izzólámpát?
d) Hosszú idő (néhány perc) elteltével ebben az esetben megállapodik-e valahol az izzószál?
Minden válaszát indokolja!

a) Az izzót hálózati feszültségre kapcsoljuk. A hálózati feszültség váltakozó. Ebből az következik, hogy az izzószálban az áram iránya folyton változik. Ha vezetékben áram folyik, akkor a körülötte mágneses mező alakul ki. Ezzel a mágneses mezővel lép kölcsönhatásba a mágnes. De mivel az áram iránya változik, a vezető körüli mágneses mező is változik. Ezért a mi mágnesünk egyszer vonzzani, egyszer taszítani fogja. Ez rezgésbe hozza az izzószálat.
b) Az izzószál nem fog megállapodni, mert mindig megváltozik a mágneses mező az izzószál körül, tehát mindig lesz vonzás és taszítás.
c) Egyenfeszültség esetén egyenáram fog folyni az izzószálban. Ennek iránya nem változik. De ebben az esetben is van mágneses mező körülötte, tehát megint lesz vonzás vagy taszítás, de csak az egyik. Tehát állandó nagyságú erő hat. (Persze az eredő erő 0, csak a mágneses erő nem 0.)
d) Az izzószál eredeti helyzetéből kitér, mert a mágnes vagy vonzotta, vagy taszította. És ebben a kitérített helyzetben is marad, mert állandó erő hat rá.
3/B A radioaktív sugárzást kibocsátó hulladékot atomtemetőben helyezzük el. A biztonságos elhelyezés érdekében egy mintán megmértük a tároló betonfalának sugárzáselnyelő képességét a falvastagság függvényében. A mellékelt táblázat mutatja, hogy egy Geiger-Müller-számlálócsővel hány részecskét detektálunk a falon kívül másodpercenként. 15 beütés/s-os sugárzásszintnél nagyobb terhelés a szabvány szerint nem érheti az emberi szervezetet.
| Falvastagság (cm) |
0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| Sugárzás a falon kívül (beütés/s) |
210 | 147 | 106 | 73 | 51 | 37 | 25 | 18 | 13 |
a) Ábrázolja a mért beütésszámokat a tároló falvastagságának függvényében!
b) Hányad részére csökkenti le az első 4 cm beton a környezetbe kijutó sugárzást?
c) Milyen vastag betonfal védi meg biztonságosan a környezetet?
d) A hulladékban lévő izotóp felezési ideje 17 év. Meghaladja-e a hulladék sugárzásszintje 50 év múlva a szabvány szerint megengedhető mértéket?
a) Ezt könnyen megtehetjük, az érettségi lapon van kockás cucc, amibe felvehetjük a táblázat pontjait. Miután a pontokat berajzoltuk, kössük is össze őket egy exponenciális jellegű vonallal. (Nekem még könnyenbb dolgom volt, mert egy ábrázoló programmal csináltam. :))
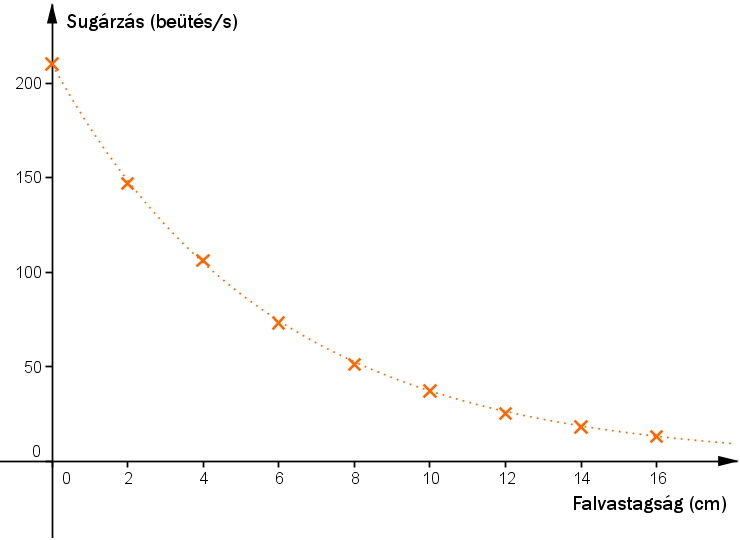
b) A táblázatból megállapítva a 4 centis fal a 210-es sugárzást 106-ra csökkenti, ami kb. a fele a 210-nek, pontosabban az 50,48%-a, tehát nyugodtan mondhatjuk, hogy a felére csökkenti.
c) A táblázatból látszik, hogy a 14 cm-es fal még nem elég, a 16 cm-es pedig már igen. Kérdés, elég lenne-e a 15 cm-es fal is? A táblázatból látszik, hogy a függvény 210-ről indul, és 4 cm-enként feleződik. Ezért ez egy olyan exponenciális függvény, ami 2 a valahanyadikon. Mivel csökken, ezért a kitevő negatív. Jelöljük x-szel a falvastagságot. Mivel 4 cm-nél feleződik először, ezért x-et 4-gyel kell osztani. Tehát a kitevőben \$-\frac x4 $\ lesz: \$2^{-\frac x4}$\. És mivel 210-ről indul, ezért 210-zel még szorozni kell: \$ 210 \cdot 2^{-\frac x4}$\. Ennek kell 15-nek lenni. Oldjuk meg x-re! $$ 210 \cdot 2^{-\frac x4}=15 \qquad /:210 $$ $$ 2^{-\frac x4}=0,0714 \qquad / \log_2 $$ $$ -\frac x4=-3,8 \qquad / \cdot (-4) $$ $$ x=15,2 $$
Tehát a 15 cm-es fal sem elég még, de 15,5 cm.es már jó. Mellesleg a hivatalos megoldás szerint legalább 15 cm-esnek kell lenni, amit a grafikon alapján kéne leolvasni. Én mindenesetre kétlem, hogy ezt a grafikonról le lehet olvasni.
d) A felezési idő pont úgy működik, mint a fal az előbbi feladatban: 17 évenként a felére csökkena sugárzás. Tehát az előző képletben x helyére írjunk t-t, a 4 helyére pedig 17-et. Ekkor az egyenlet: $$ 210 \cdot 2^{-\frac {t}{17}}=15 \qquad /:210 $$ $$ 2^{-\frac {t}{17}}=0,0714 \qquad / \log_2 $$ $$ -\frac {t}{17}=-3,8 \qquad / \cdot (-17) $$ $$ t=64,6 $$
Tehát 64,6 év múlva csökken a megfelelő szint alá, így az 50 év még kevés.
